Условия.на весах стоит высокий сосуд,частично наполненный жидкостью.с нити в жидкость опускают брусок так,чтобы он был погружен на половину своего объем,но при это не касается ни стенок,ни дна сосуда.масса сосуда с жидкостью составляет m= 430 г ,а масса бруска - 0,6m.определите показания весов ,если плотность материала бруска в 1,5 раза больше плотности жидкости.ответ выразите в г,округлив до целых
Действуя на длинное плечо рычага, мы выигрываем в силе, но при этом во столько же проигрываем в пути.
A₁=F₁S₁, A₂=F₂S₂
F₁>F₂, S₁>S₂
S₁/S₂ = F₂/F₁
F₁S₁=F₂S₂
A₁=A₂, из чего следует, что рычаг не даёт выигрыша в работе.
2. Неподвижный блок.
S₁=S₂, F₁=F₂
A₁=F₁S₁, A₂=F₂S₂
A₁=A₂, из чего следует, что неподвижный блок не даёт выигрыша в работе.
3. Подвижный блок.
S₁=h, S₂=2h
F₁=P, F₂=P/2
A₁=Ph, A₂=P/2 * 2h = Ph
A₁=A₂, из чего следует, что подвижный блок не даёт выигрыша в работе.
Простые механизмы не дают выигрыша в работе.
Получая выигрыш в силе в 2 раза, проигрывают в 2 раза в пути.
"Золотое правило механики":
Во сколько раз выигрываем в силе, во столько раз проигрываем в расстоянии.
Р2 = 328 Н
Объяснение:
Давай немного теории:
Сила, с которой тело давит на опору , называют весом.
Вес тела обозначают P и измеряют в ньютонах ( H ).
Ну а в вообще любую силу обозначают через F . То есть в данном случае можно хоть так хоть эдак.
Произведение модуля силы, вращающей тело, на её плечо называется моментом силы.
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по часовой стрелке, равен моменту силы, вращающей его против часовой стрелки.
Это правило, называемое правилом моментов, можно записать в виде формулы: M1=M2 .
Момент силы M = F · L
У нас два момента М1 и М2
M1 = F1 · L1
M2= F2 · L2
Ну и приравниваем их так как моменты всё же РАВНЫ
F1 · L1 = F2 · L2
Подставляем числа
82 * 8 = F2 * 2 (расстояния L1 и L2 подсчитываем на рисунке)
F2 =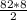
F2 = 82*4
F2 = 328 Н