Объяснение:
ДАНО:
мл
_______________
- ?
Давление жидкости равно ее весу, деленному на площадь:
Учитывая, что P = mg, то
Выражая массу через плотность и объём и подставляя в , имеем
m = ρV
и
= ρ/S
В нашем случае:
ρg/S (1)
= ρg/S (2)
Найдем отношение уравнения (2) к уравнению (1):
/ = ρg/S / ρg/S.
Учитывая, что и сокращения на ρ, g, S, получим:
то есть объём жидкости увеличился в 3 раза составляет:
50 мл · 3 = 150 мл
Таким образом, в цилиндр нужно долить:
= 150мл - 50 мл = 100 мл.
ответ: 100 мл
Объяснение:
ДАНО:
_______________
Давление жидкости равно ее весу, деленному на площадь:
Учитывая, что P = mg, то
Выражая массу через плотность и объём и подставляя в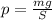
, имеем
m = ρV
и
В нашем случае:
и
Найдем отношение уравнения (2) к уравнению (1):
Учитывая, что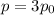
и сокращения на ρ, g, S, получим:
то есть объём жидкости увеличился в 3 раза составляет:
50 мл · 3 = 150 мл
Таким образом, в цилиндр нужно долить:
ответ: 100 мл
Vср = S / t.
Рассмотрим первую половину пути:
S₁ = (S/2)
t₁ = S₁/V₁ = S / (2*V₁) = S / 20 = (1/20)*S = 0,05*S ч
Рассмотрим вторую половину пути.
Оставшийся путь
S₂ = (S/2)
Оставшееся время t₂ разобьем на 3 равных промежутка по (t₂ /3) часа
Путь на первой трети остатка:
S₂₁ = V₂₁*(t₂/3) = (20/3)*t₂
Путь на второй трети остатка:
S₂₂ = 0 (ремонт!)
Путь на последней трети остатка:
S₂₃ = V₂₃*(t₂/3) = (5/3)*t₂
Собираем
S₂ = S₂₁+S₂₂+S₂₃ = (20/3)*t₂ + 0 + (5/3)*t₂ = (25/3)*t₂
(S/2) = (25/3)*t₂
t₂ = (3/50)*S = 0,06*S ч
Общее время:
t = t₁ +t₂ = 0,05*S + 0,06*S = 0,11*S
Средняя скорость:
Vcp = S / (0,11*S) = 1 / 0,11 ≈ 9 км/ч