Направим ось OY вертикально вверх, а ось OX горизонтально вдоль направления броска. Начало координат совместим с начальным положением тела. Система координат XOY жёстко связана с землёй.
1. Сначала найдем дальность полёта. Для этого сначала найдем время полёта.
поэтому сократим равенство на t,
(V)
Подставим в последнее t из (V):
т.к. sin(2α) = 2sin(α)cos(α).
Итак,
x = 12²(м/с)²·sin(2·60°)/(10м/с²) = 144·sin(120°)/10 (м) = 14,4·sin(90°+30°) (м) =
= 14,4·cos(30°) м = 14,4·(√3)/2 м ≈ 12,5 м
2. Найдем высоту подъёма. Для этого найдем время подъёма.
На максимальной высоте очевидно будет , поэтому
(W)
Подставляем сюда значение t из (W):
Итак,
y = 12²(м/с)²·sin²(60°)/(2·10м/с²) = 144·( (√3)/2 )²/ 20 (м) =
Дано: v₀ = 12 м/с, α = 60°, g = 10 м/с²
Направим ось OY вертикально вверх, а ось OX горизонтально вдоль направления броска. Начало координат совместим с начальным положением тела. Система координат XOY жёстко связана с землёй.
1. Сначала найдем дальность полёта. Для этого сначала найдем время полёта.
Подставим в последнее t из (V):
т.к. sin(2α) = 2sin(α)cos(α).
Итак,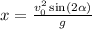
x = 12²(м/с)²·sin(2·60°)/(10м/с²) = 144·sin(120°)/10 (м) = 14,4·sin(90°+30°) (м) =
= 14,4·cos(30°) м = 14,4·(√3)/2 м ≈ 12,5 м
2. Найдем высоту подъёма. Для этого найдем время подъёма.
На максимальной высоте очевидно будет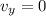 , поэтому
, поэтому
Подставляем сюда значение t из (W):
Итак,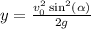
y = 12²(м/с)²·sin²(60°)/(2·10м/с²) = 144·( (√3)/2 )²/ 20 (м) =
= 7,2·3/4 (м) = 5,4 м.