Так как ничего не сказано, в какой точке системы координат находится ковбой изначально, и угол φ<360° говорит о произвольном направлении, то этот угол может быть каким угодно. Например, на рис.1 ковбой начал скакать из точки A под углом φ=90°, в точке М повернул налево под прямым углом и оказался в точке F с заданными координатами. А на рис.2 ковбой начал скакать из точки В под углом φ=45°, повернул налево под прямым углом в точке N и оказался в точке F, выполнив все условия задачи. Треугольники AMF и BNF можно вращать около точки F на любой угол, соответственно будет меняться угол φ. Вывод : если не заданы начальные координаты ковбоя, то угол φ может быть каким угодно.
Пусть ковбой начинает свой путь из точки начала координат О(0;0) - рис.3. Проскакав OP=6 км под углом φ к оси x, ковбой повернул налево под прямым углом в точке P и проскакал ещё PF=8 км.
Координаты точки F(-5; y>0).
ΔOPF : ∠P = 90°; OP = 6 км; PF = 8 км. Теорема Пифагора :
OF² = OP² + PF² = 6² + 8² = 100 = 10²
OF = 10 км - перемещение ковбоя
sin ∠FOP = PF/OF = 8/10 = 0,8 ⇒ ∠FOP = arcsin 0,8
ΔONF : ∠N = 90°; ON = 5 км; OF = 10 км - катет равен половине гипотенузы ⇒ ∠OFN = 30° ⇒ ∠NOF = 60°
ΔT=100,1 К
Объяснение:
Первое начало термодинамики
Q=A+ΔU
Если считать, что общее количество тепла, полученное газом, за весь процесс равно 416 Дж, то
Q=Q12+Q23+Q34
рассмотрим
Q12=A12+ΔU12. A=pΔV, т.к. ΔV=0 ⇒ A=0 ⇒Q12=ΔU12=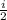
*v*R*ΔT
Q23=A12+ΔU12 Работа газом совершена отрицательная, и ΔT <0
Q23=-A12+-ΔU12=-pΔV-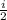
*v*R*ΔT
из ур Менделеева-Клапейрона
pΔV=v*R*ΔT, тогда
Q23=-A12+-ΔU12=-v*R*ΔT-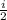
*v*R*ΔT=- 
*v*R*ΔT
Q34=A34+ΔU34. A=pΔV, т.к. ΔV=0 ⇒ A=0 ⇒Q34=ΔU34=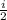
*v*R*ΔT
Q=Q12+Q23+Q34=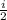
*v*R*ΔT- 
*v*R*ΔT+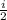
*v*R*ΔT=v*R*ΔT*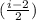
Отсюда
ΔT=Q/(v*R*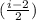
)
если газ одноатомный, то i=3, но про это в условии не сказано
ΔT=416/(1*8,31*0,5)=100,1 К
Так как ничего не сказано, в какой точке системы координат находится ковбой изначально, и угол φ<360° говорит о произвольном направлении, то этот угол может быть каким угодно. Например, на рис.1 ковбой начал скакать из точки A под углом φ=90°, в точке М повернул налево под прямым углом и оказался в точке F с заданными координатами. А на рис.2 ковбой начал скакать из точки В под углом φ=45°, повернул налево под прямым углом в точке N и оказался в точке F, выполнив все условия задачи. Треугольники AMF и BNF можно вращать около точки F на любой угол, соответственно будет меняться угол φ. Вывод : если не заданы начальные координаты ковбоя, то угол φ может быть каким угодно.
==================================================
Пусть ковбой начинает свой путь из точки начала координат О(0;0) - рис.3. Проскакав OP=6 км под углом φ к оси x, ковбой повернул налево под прямым углом в точке P и проскакал ещё PF=8 км.
Координаты точки F(-5; y>0).
ΔOPF : ∠P = 90°; OP = 6 км; PF = 8 км. Теорема Пифагора :
OF² = OP² + PF² = 6² + 8² = 100 = 10²
OF = 10 км - перемещение ковбоя
sin ∠FOP = PF/OF = 8/10 = 0,8 ⇒ ∠FOP = arcsin 0,8
ΔONF : ∠N = 90°; ON = 5 км; OF = 10 км - катет равен половине гипотенузы ⇒ ∠OFN = 30° ⇒ ∠NOF = 60°
∠NOF + ∠FOP + φ = 180°
φ = 180° - ∠NOF - ∠FOP = 180° - 60° - arcsin 0,8 ≈
≈ 120° - 53,131° ≈ 66,869° ≈ 66,9°
ответ : φ ≈ 66,9°