Надеюсь, масса стержня равна 2 кг, а не двум метрам. Также будем считать, что грузы закреплены на концах стержня.
Рычаг находится в равновесии, если сумма моментов сил (с учётом знака), приложенных к нему, равна нулю. Следовательно, сумма моментов сил равна нулю. ))) Мы имеем следующую картину маслом. (См. рисунок "рычаг") Точка С - это точка крепления нити к стержню. Это и есть точка подвеса, относительно которой всё и будем считать. Пусть O - это центр масс стержня. Силу тяжести, действующую на стержень, надо не потерять для правильного решения задачи. Пусть x - это расстояние от точки O до точки С. (на картинке не обозначил)
Обозначим расстояния от точки С до грузов латинскими соответственно. В результате, мы получаем систему линейных уравнений. Три неизвестных 2 уравнения. Задача не имеет однозначного решения. Криво сформулирована задача, перепроверь условия, либо допиши ещё данных. Пример, пусть Тогда первое равенство выполняется, следовательно x = (0,4*1-0,1*2)/2=0,1. То есть в этом случае место крепления груза 2 совпадёт с центром масс стержня. Пусть Тогда первое равенство выполняется, следовательно x = (0,35*1-0,15*2)/2=0,025. И так разные варианты можно перебирать до бесконечности.
Оба приведённых примера подходят к условиям задачи в качестве ответа.
Пусть α — угол наклона плоскости. Сила нормального давления бруска на плоскость После увеличения угла наклона плоскости брусок остался в покое, значит, сила нормального давления бруска по прежнему рассчитывается по приведённой формуле. При увеличении угла косинус угла уменьшается, следовательно, сила нормального давления уменьшается. Коэффициент трения бруска о плоскость не зависит от угла наклона плоскости, а только от свойств поверхности, поэтому он не изменяется.
Надеюсь, масса стержня равна 2 кг, а не двум метрам.
Также будем считать, что грузы закреплены на концах стержня.
Рычаг находится в равновесии, если сумма моментов сил (с учётом знака), приложенных к нему, равна нулю.
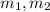латинскими 
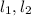соответственно.
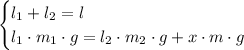
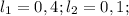
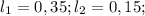
Следовательно, сумма моментов сил равна нулю. )))
Мы имеем следующую картину маслом. (См. рисунок "рычаг")
Точка С - это точка крепления нити к стержню. Это и есть точка подвеса, относительно которой всё и будем считать.
Пусть O - это центр масс стержня. Силу тяжести, действующую на стержень, надо не потерять для правильного решения задачи.
Пусть x - это расстояние от точки O до точки С. (на картинке не обозначил)
Обозначим расстояния от точки С до грузов
В результате, мы получаем систему линейных уравнений.
Три неизвестных 2 уравнения. Задача не имеет однозначного решения.
Криво сформулирована задача, перепроверь условия, либо допиши ещё данных.
Пример, пусть
Тогда первое равенство выполняется, следовательно x = (0,4*1-0,1*2)/2=0,1.
То есть в этом случае место крепления груза 2 совпадёт с центром масс стержня.
Пусть
Тогда первое равенство выполняется, следовательно x = (0,35*1-0,15*2)/2=0,025.
И так разные варианты можно перебирать до бесконечности.
Оба приведённых примера подходят к условиям задачи в качестве ответа.
Пусть α — угол наклона плоскости. Сила нормального давления бруска на плоскость После увеличения угла наклона плоскости брусок остался в покое, значит, сила нормального давления бруска по прежнему рассчитывается по приведённой формуле. При увеличении угла косинус угла уменьшается, следовательно, сила нормального давления уменьшается. Коэффициент трения бруска о плоскость не зависит от угла наклона плоскости, а только от свойств поверхности, поэтому он не изменяется.