Относительная влажность воздуха в помещении при температуре 20 °c равна 70%. пользуясь таблицей плотности насыщенных паров воды, определите массу воды в кубическом метре помещения.
Не могу сейчас сам решить, но нашел похожую задачку под номером 1). Просто замени данные под свои
Для нагрева до температуры кипения требуется количество теплоты Q1=c*m*(t2-t1), где с=4200 Дж/(кг*град)-удельная теплоемкость воды, m=700 г = 0.7 кг-масса воды, t2=100°С - конечная температура, t1=20°С-начальная температура. Q1=4200*0.7*(100-20)=240000 Дж = 0.24 МДж.
Для превращения в пар требуется количество теплоты Q2=L*m, где L=2.3*10^6 Дж - удельная теплота парообразования воды. Q2=0.7*2.3*10^6 = 1.61*10^6 Дж = 1.61МДж.
Полное количество теплоты Q=Q1+Q2=0.24+1.61=1.85 МДж.
Если решать эту задачу по школьному, без привлечения инструментария матанализа, то рассуждать можно следующим образом, - в любой точке траектории ускорение свободного падения может быть разложено на две составляющих - вдоль касательной к траектории (нормальное ускорение) и вдоль нормали к траектории (центростремительное ускорение), нам нужна вторая величина, так как она позволяет рассчитать искомый радиус. В наивысшей точке подъема мяча, очевидно, что центростремительное ускорение целиком совпадает с ускорением свободного падения:
Откуда:
Горизонтальная составляющая скорости будет везде одинакова и равна (учтем что 54 км/ч=15 м/с):
Объяснение:
Не могу сейчас сам решить, но нашел похожую задачку под номером 1). Просто замени данные под свои
Для нагрева до температуры кипения требуется количество теплоты Q1=c*m*(t2-t1), где с=4200 Дж/(кг*град)-удельная теплоемкость воды, m=700 г = 0.7 кг-масса воды, t2=100°С - конечная температура, t1=20°С-начальная температура. Q1=4200*0.7*(100-20)=240000 Дж = 0.24 МДж.
Для превращения в пар требуется количество теплоты Q2=L*m, где L=2.3*10^6 Дж - удельная теплота парообразования воды. Q2=0.7*2.3*10^6 = 1.61*10^6 Дж = 1.61МДж.
Полное количество теплоты Q=Q1+Q2=0.24+1.61=1.85 МДж.
11,25 м
Объяснение:
Если решать эту задачу по школьному, без привлечения инструментария матанализа, то рассуждать можно следующим образом, - в любой точке траектории ускорение свободного падения может быть разложено на две составляющих - вдоль касательной к траектории (нормальное ускорение) и вдоль нормали к траектории (центростремительное ускорение), нам нужна вторая величина, так как она позволяет рассчитать искомый радиус. В наивысшей точке подъема мяча, очевидно, что центростремительное ускорение целиком совпадает с ускорением свободного падения:
Откуда:
Горизонтальная составляющая скорости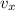
будет везде одинакова и равна (учтем что 54 км/ч=15 м/с):
Искомый радиус кривизны траектории: