В случае если бруски заведомо одинакового размера, то есть равны их объемы, но плотность мрамора больше, чем плотность парафина.
Если брать в оборот что парафиновый брусок в три раза выше мраморного, определить его потенциальную массу очень легко, пользуясь удельным весом мрамора и парафина:
Парафин - 870 на 1 метр в кубе (кг)
Мрамор - 2600 на один метр в кубе (кг)
Чисто на примере условных единиц:
(Мрамора) = 10*1*2600 = 26000 усл. ед.
(Парафина) = 10*3*870 = 26100 усл. ед.
Для замены условных единиц обратитесь в таблицу плотностей в конце учебника или на интернет-ресурсах.
Таким образом мы выяснили что потенциальная энергия парафина немного больше, чем энергия мрамора.
Решение: т. к. шар не тонет и не всплывает. - объём тела пополам т. к. сила Архимеда действует только на погруженную в воду часть, а по условию шар наполовину погружен в воду. - обе части уравнения делим на и на - домножаем обе части уравнения на - сделаем уравнение привычнее - из уравнения выразим формулу Так как ничего про массу воздуха в полости не сказано, предположим, что там вакуум и для того, чтобы найти объём стеклянной части шара возьмём массу всего шара, а не стекла:
ответ: (может отличатся в связи с различной плотностью стекла, я взял плотность оконного)
Формула Потенциальной энергии =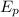 = g·m·h
= g·m·h
В случае если бруски заведомо одинакового размера, то есть равны их объемы, но плотность мрамора больше, чем плотность парафина.
Если брать в оборот что парафиновый брусок в три раза выше мраморного, определить его потенциальную массу очень легко, пользуясь удельным весом мрамора и парафина:
Парафин - 870 на 1 метр в кубе (кг)
Мрамор - 2600 на один метр в кубе (кг)
Чисто на примере условных единиц:
Для замены условных единиц обратитесь в таблицу плотностей в конце учебника или на интернет-ресурсах.
Таким образом мы выяснили что потенциальная энергия парафина немного больше, чем энергия мрамора.
Решение:
Так как ничего про массу воздуха в полости не сказано, предположим, что там вакуум и для того, чтобы найти объём стеклянной части шара возьмём массу всего шара, а не стекла:
ответ: