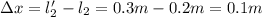1) Не очень понятно, что есть трос, но, вероятно, он соединяет груз и стержень. Тогда сила натяжения по 2 зак. Ньютона будет равна силе тяжести груза:
2) Так как сила тяжести стержня должна прикладываться к центру масс, а он располагается посередине стрежня. Вспомним правило моментов, согласно которому произведение сил на их плечи должны быть равны (силы тяжести стержня и силы натяжения троса).
Так как сила тяжести стержня равна
А это в два раза меньше меньше силы натяжения, то плечо силы тяжести должно быть в два раза больше плеча силы натяжения. Если точка опоры стоит по одну сторону от центра и края, где весит груз, то плечо силы тяжести всегда меньше плеча силы натяжения. Значит, точка опоры лежит между центром и краем. Данное расстояние равно . Тогда имеем систему уравнений:
Решения ее:
Тогда расстояние от конца, где прикреплен груз, равно - равно 0,2м. Расстояние от другого конца это = 1м
3)Решение аналогично пункту 2:
Так как сила тяжести стержня должна прикладываться к центру масс, а он располагается посередине стрежня. Вспомним правило моментов, согласно которому произведение сил на их плечи должны быть равны (силы тяжести стержня и силы натяжения троса).
Так как сила тяжести стержня равна
А это численно равно силе натяжения, следовательно, плечо силы тяжести должно быть равно плечу силы натяжения. Если точка опоры стоит по одну сторону от центра и края, где весит груз, то плечо силы тяжести всегда меньше плеча силы натяжения. Значит, точка опоры лежит между центром и краем. Данное расстояние равно . Тогда имеем систему уравнений:
R(₅,₆)=(R₅*R₆):(R₅+R₆)=(25*100):(25+100)=20 Ом;
R(₄-₆)=R₄+R(₅,₆)=10+20=30 Ом;
R₃=R(₄-₆)=30 Ом =>
R(₃-₆)=R₃/2=R(₄-₆)/2=30/2=15 Ом;
R(₂-₆)=R₂+R(₃-₆)=5+15=20 Ом;
R₁=R(₂-₆)=20 Ом =>
Rобщ=Rᴀв=R(₁-₆)=R₁/2=R(₂-₆)/2=20/2=10 Ом;
Rэкв=Rᴀв+r₀=10+0,5=10,5 Ом;
I=ℰ/Rэкв=210/10,5=20 A;
Uᴀв=U₁=ℰ-I*r₀=210-20*0,5=200 B;
I₁=U₁/R₁=200/20=10 A;
I₂=I-I₁=20-10=10 A;
U₂=I₂*R₂=10*5=50 B;
U₃=U₁-U₂=200-50=150 B;
I₃=U₃/R₃=150/30=5 A;
I₄=I₂-I₃=10-5=5 А;
U₄=I₄*R₄=5*10=50 B;
Uᴇғ=U₅=U₆=U₃-U₄=150-50=100 B;
I₅=Uᴇғ/R₅=100/25=4 A;
I₆=Uᴇғ/R₆=100/100=1 A;
P=Uᴀв*I=200*20=4000 Вт=4 кВт;
ΣP=I₁²*R₁+I₂²*R₂+I₃²*R₃+I₄²*R₄+I₅²*R₅+I₆²*R₆=
=10²*20+10²*5+5²*30+5²*10+4²*25+1²*100=
=2000+500+750+250+400+100=4000 Вт=4 кВт.
Т.к. P=ΣP=4 кВт, то считаем, что баланс
мощностей имеет место быть.
P.S. И вся эта красота за какие-то 5 б.
Объяснение:
ДАНО:
-----------------------------
1) Не очень понятно, что есть трос, но, вероятно, он соединяет груз и стержень. Тогда сила натяжения по 2 зак. Ньютона будет равна силе тяжести груза:
2) Так как сила тяжести стержня должна прикладываться к центру масс, а он располагается посередине стрежня. Вспомним правило моментов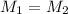 , согласно которому произведение сил на их плечи должны быть равны (силы тяжести стержня и силы натяжения троса).
, согласно которому произведение сил на их плечи должны быть равны (силы тяжести стержня и силы натяжения троса).
Так как сила тяжести стержня равна
А это в два раза меньше меньше силы натяжения, то плечо силы тяжести должно быть в два раза больше плеча силы натяжения. Если точка опоры стоит по одну сторону от центра и края, где весит груз, то плечо силы тяжести всегда меньше плеча силы натяжения. Значит, точка опоры лежит между центром и краем. Данное расстояние равно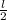 . Тогда имеем систему уравнений:
. Тогда имеем систему уравнений:
Решения ее:
Тогда расстояние от конца, где прикреплен груз, равно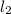 - равно 0,2м. Расстояние от другого конца это
- равно 0,2м. Расстояние от другого конца это  = 1м
= 1м
3)Решение аналогично пункту 2:
Так как сила тяжести стержня должна прикладываться к центру масс, а он располагается посередине стрежня. Вспомним правило моментов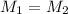 , согласно которому произведение сил на их плечи должны быть равны (силы тяжести стержня и силы натяжения троса).
, согласно которому произведение сил на их плечи должны быть равны (силы тяжести стержня и силы натяжения троса).
Так как сила тяжести стержня равна
А это численно равно силе натяжения, следовательно, плечо силы тяжести должно быть равно плечу силы натяжения. Если точка опоры стоит по одну сторону от центра и края, где весит груз, то плечо силы тяжести всегда меньше плеча силы натяжения. Значит, точка опоры лежит между центром и краем. Данное расстояние равно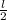 . Тогда имеем систему уравнений:
. Тогда имеем систему уравнений:
Решения ее:
Тогда переместить ее надо на