Итак источник ЭДС имеет параметры: E=6 В, R_вн=1 Ом.
2. Запишем формулу (функцию) зависимости мощности, выделяемой на нагрузке, от величины сопротивления нагрузки:
Pн=f(Rн).
Распишем:
Pн=Iн²*Rн;
Iн=E/(Rн+R_вн);
Pн=(E²/(Rн+R_вн))²*Rн.
Pн=E²*Rн/(Rн+R_вн)²
Функция нелинейная. Найдем ее максимальное значение на промежутке Rн∈[0;+∝).
Функция имеет наибольшее (наименьшее) значение на интервале или в конечных точках интервала, или в точках экстремума всередине интервала. При Rн=0 Pн=0 (мощности не на чем выделяться). При Rн→∞ мощность стремиться к 0, т.к. ток через нагрузку стремится к 0. Найдем точку или точки экстремума:
R_вн=Rн при этом значении Rн функция имеет экстремум!
Определим характер экстремума:
При Rн<R_вн производная имеет знак "+";
При Rн>R_вн производная имеет знак "-";
Производная в искомой точке меняет знак с "+" на "-", следовательно это - максимум функции!
Т.О. видим, что максимальная мощность, а, следовательно, и максимальное количество тепла на сопротивлении нагрузки выделится, если сопротивление нагрузки равно внутреннему сопротивлению источника ЭДС! Говорят "нагрузка согласована с источником"!
Максимальное значение 9 Вт
Объяснение:
Да, все, конечно, по закону Ома. Но чуть сложнее.
Применяемые величины и обозначения:
R_вн - внутреннее сопротивление источника ЭДС, Ом
Rн - сопротивление нагрузки, Ом
E - ЭДС, В
Iн - ток нагрузки, А
Pн - мощность нагрузки, Вт
1. Определим параметры источника ЭДС( величину R_вн и Е). Для этого запишем уравнения:
Источник ЭДС Е нагружен на сопротивление Rн=5 Ом, при этом течет ток Iн=1 А. По закону Ома:
E=Iн(Rн+R_вн);
E=1(5+R_вн);
Источник ЭДС в режиме короткого замыкания, Rн=0, I=6 А.
E=6(R_вн);
Решаем систему уравнений:
E=1(5+R_вн); ⇔ 6R_вн=1(5+R_вн);⇔ 6R_вн-R_вн=5 ⇔ R_вн=1 (Ом).
E=6(R_вн); ⇔ E=6*1=6; E=6 (В).
Итак источник ЭДС имеет параметры: E=6 В, R_вн=1 Ом.
2. Запишем формулу (функцию) зависимости мощности, выделяемой на нагрузке, от величины сопротивления нагрузки:
Pн=f(Rн).
Распишем:
Pн=Iн²*Rн;
Iн=E/(Rн+R_вн);
Pн=(E²/(Rн+R_вн))²*Rн.
Pн=E²*Rн/(Rн+R_вн)²
Функция нелинейная. Найдем ее максимальное значение на промежутке Rн∈[0;+∝).
Функция имеет наибольшее (наименьшее) значение на интервале или в конечных точках интервала, или в точках экстремума всередине интервала. При Rн=0 Pн=0 (мощности не на чем выделяться). При Rн→∞ мощность стремиться к 0, т.к. ток через нагрузку стремится к 0. Найдем точку или точки экстремума:
Возьмем производную:
Pн'=[E²*Rн/(Rн+R_вн)²]';
учитывая, что E и R_вн - здесь постоянные:
Pн'=E²(Rн*(Rн+R_вн)⁻²)'=E²*[1*(Rн+R_вн)⁻²+Rн(-2*(Rн+R_вн)⁻³)]=E²*[(Rн+R_вн)⁻²-2Rн(Rн+R_вн)⁻³)]=E²[(R_вн-Rн)/(Rн+R_вн)³];
Pн'=E²[(R_вн-Rн)/(Rн+R_вн)³];
Приравняем производную к 0
Pн'=0;
E²[(R_вн-Rн)/(Rн+R_вн)³]=0;
E²≠0; (R_вн-Rн)=0;/(Rн+R_вн)³≠0.
R_вн=Rн при этом значении Rн функция имеет экстремум!
Определим характер экстремума:
При Rн<R_вн производная имеет знак "+";
При Rн>R_вн производная имеет знак "-";
Производная в искомой точке меняет знак с "+" на "-", следовательно это - максимум функции!
Т.О. видим, что максимальная мощность, а, следовательно, и максимальное количество тепла на сопротивлении нагрузки выделится, если сопротивление нагрузки равно внутреннему сопротивлению источника ЭДС! Говорят "нагрузка согласована с источником"!
Посчитаем.
Rн=R_вн;
Rн=1 Ом.
Pн=[E/(R_вн+Rн)]²*Rн;
Pн=6²/(1+1)²*1=36/4=9 (Вт). - максимальное значение!
Проверим:
1) Rн>R_вн; Rн=1,1 Ом; Pн=[E/(R_вн+Rн)]²*Rн; Pн=[6/(1+1,1)]²*1,1=36*1,1/2,1²=8,9 (Вт)<9
2) Rн<R_вн; Rн=0.9 Ом;
Pн=[E/(R_вн+Rн)]²*Rн;Pн=36/(1+0,9)]²*0.9=36*0.9/1,9²=8,97 (Вт)<9
-5 А; -3 А; 8 А
6 В; -86 В; 12 В
683 Вт
Объяснение:
Воспользуемся методом наложения токов:
- активен только источник Е1
Примем потенциал точки а за ноль для удобства, тогда:
Токи через оставшиеся ветви:
Аналогично находим токи для случая активных источников E2 и E3 (см. рисунок).
Накладываем токи друг на друга:
- ток через R1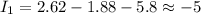
А (направлен вверх)
- ток через R2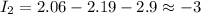
А
- ток через R3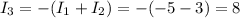
А
Значения напряжения:
Баланс мощностей: