Две пробирки вращаются в одной центрифуге. При этом, скорость одной равна 56 м/с, а скорость второй 34 м/с. Окружность какого радиуса описывает первая пробирка, если вторая расположена на 11 см ближе к центру центрифуги? ответ приведите в см.
Данные пробирки имеют одинаковую частоту вращения, но разные линейные скорости, так как одна пробирка находится дальше другой от центра центрифуги. Пусть r₁ = R – радиус окружности, описываемый первой пробиркой, тогда r₂ = (R - 11) – это радиус окружности, по какой движется вторая пробиркой. Циклические частоты пробирок одинаковы ⇒ ω₁ = ω₂, а линейные скорости по условию равны: v₁ = 56 м/с, v₂ = 34 м/с
По формуле из кинематики: v₁ = ω₁·r₁, v₂ = ω₂·r₂ ⇒ ω₁ = v₁/r₁ = ω₂ = v₂/r₂ ⇒ v₁/R = v₂/(R - 11) ⇒ (по правилу пропорции) v₁ · (R - 11) = v₂ · R ⇒
R · (v₁ - v₂) = 11 · v₁ ⇒ R = сантиметров
ответ: первая пробирка описывает окружность радиусом в 28 см.
Данные пробирки имеют одинаковую частоту вращения, но разные линейные скорости, так как одна пробирка находится дальше другой от центра центрифуги. Пусть r₁ = R – радиус окружности, описываемый первой пробиркой, тогда r₂ = (R - 11) – это радиус окружности, по какой движется вторая пробиркой. Циклические частоты пробирок одинаковы ⇒ ω₁ = ω₂, а линейные скорости по условию равны: v₁ = 56 м/с, v₂ = 34 м/с
По формуле из кинематики: v₁ = ω₁·r₁, v₂ = ω₂·r₂ ⇒ ω₁ = v₁/r₁ = ω₂ = v₂/r₂ ⇒ v₁/R = v₂/(R - 11) ⇒ (по правилу пропорции) v₁ · (R - 11) = v₂ · R ⇒
R · (v₁ - v₂) = 11 · v₁ ⇒ R =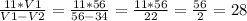 сантиметров
сантиметров
ответ: первая пробирка описывает окружность радиусом в 28 см.