Два автомобиля движутся в одном и том же направлении со скоростями υ1 и υ2 относительно поверхности Земли. Чему равна скорость света фар первого автомобиля в системе отсчета, связанной с другим автомобилем?
Равноускоренное движение — движение, при котором ненулевой вектор ускорения остаётся неизменным по модулю и направлению.
Примером такого движения является движение тела, брошенного под углом  к горизонту в однородном поле силы тяжести — тело движется с постоянным ускорением , направленным вертикально вниз.
При равноускоренном движении по прямой скорость тела определяется формулой:

Зная, что , найдём формулу для определения координаты x:

Примечание. Равнозамедленнымможно назвать движение, при котором модуль скорости равномерно уменьшается со временем (если вектора  и противонаправлены). Равнозамедленное движение также является равноускоренным.
1. Тело движется против силы притяжения, его движение - равнозамедленное. Тогда высота, на которой тело будет находиться в момент времени t, будет выражаться формулой:
2. Чтобы найти из (1) время нужно решить квадратное уравнение относительно t:
3. Таким образом получаем два решения, потому как дело достигнет высоты 10 метров дважды - во время подъёма до максимальной высоты и во время падения. Нас интересует первое прохождение данной отметки, поэтому вычислим меньшее из значений:
Примером такого движения является движение тела, брошенного под углом  к горизонту в однородном поле силы тяжести — тело движется с постоянным ускорением , направленным вертикально вниз.
При равноускоренном движении по прямой скорость тела определяется формулой:

Зная, что , найдём формулу для определения координаты x:

Примечание. Равнозамедленнымможно назвать движение, при котором модуль скорости равномерно уменьшается со временем (если вектора  и противонаправлены). Равнозамедленное движение также является равноускоренным.
Начальная скорость: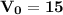 м/с.
м/с.
Высота: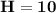 м.
м.
Найти нужно время:
Решение:1. Тело движется против силы притяжения, его движение - равнозамедленное. Тогда высота, на которой тело будет находиться в момент времени t, будет выражаться формулой: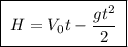
2. Чтобы найти из (1) время нужно решить квадратное уравнение относительно t:
3. Таким образом получаем два решения, потому как дело достигнет высоты 10 метров дважды - во время подъёма до максимальной высоты и во время падения. Нас интересует первое прохождение данной отметки, поэтому вычислим меньшее из значений: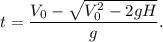
Численно получим: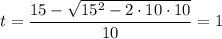 (c).
(c).
ответ: через 1 с.