один із фундаментальних законів фізики, який стверджує, що у замкненій системі сумарний імпульс усіх тіл зберігається. Він звучить так: У замкненій системі геометрична сума імпульсів залишається сталою при будь-яких взаємодіях тіл цієї системи між собою.
Якщо на систему тіл зовнішні сили не діють або вони врівноважені, то така система називається замкненою, для неї виконується закон збереження імпульсу: повний імпульс замкненої системи тіл залишається незмінним за будь-яких взаємодій тіл цієї системи між собою:
Закон збереження імпульсу є наслідком однорідност Объяснение:
Пусть рассматривается движение двух шаров под номерами 1 и 2. Выберем такую систему отсчета, в которой скорость второго шарика равна нулю. Пусть также - векторы скоростей первого шарика до и после столкновения соответственно. Точно также определим ; Понятно, что удар нецентральный, иначе никакого угла и не было бы. Запишем закон сохранения импульса, с учетом ("масса" сократится): ; Теперь возведем обе части в квадрат: ; Теперь запишем закон сохранения энергии (сократив на массу):
; Сравнивая полученные выражения, приходим к выводу, что , что в общем-то и требовалось
один із фундаментальних законів фізики, який стверджує, що у замкненій системі сумарний імпульс усіх тіл зберігається. Він звучить так: У замкненій системі геометрична сума імпульсів залишається сталою при будь-яких взаємодіях тіл цієї системи між собою.
Якщо на систему тіл зовнішні сили не діють або вони врівноважені, то така система називається замкненою, для неї виконується закон збереження імпульсу: повний імпульс замкненої системи тіл залишається незмінним за будь-яких взаємодій тіл цієї системи між собою:
Закон збереження імпульсу є наслідком однорідност Объяснение:
Пусть рассматривается движение двух шаров под номерами 1 и 2. Выберем такую систему отсчета, в которой скорость второго шарика равна нулю. Пусть также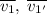 - векторы скоростей первого шарика до и после столкновения соответственно. Точно также определим
- векторы скоростей первого шарика до и после столкновения соответственно. Точно также определим 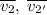 ; Понятно, что удар нецентральный, иначе никакого угла и не было бы. Запишем закон сохранения импульса, с учетом
; Понятно, что удар нецентральный, иначе никакого угла и не было бы. Запишем закон сохранения импульса, с учетом 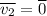 ("масса" сократится):
("масса" сократится): 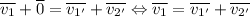 ; Теперь возведем обе части в квадрат:
; Теперь возведем обе части в квадрат: 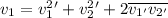 ; Теперь запишем закон сохранения энергии (сократив на массу):
; Теперь запишем закон сохранения энергии (сократив на массу):