Представим шар, который висит на нити, на него действует сила тяжести mg, которая направлена вниз, и сила натяжения нити T, направленная вверх. Запишем это в формулу:
T1=mg;( Уравнение 1).
Когда же поднесли второй шарик, то на первый уже действует 3 силы:
Сила натяжения нити, сила тяжести и Кулонова сила (Fк). Тогда уравнение примет вид:
T2=mg-Fк.(Уравнение 2).
Т.к. известно, что T2=T1/4, мы можем поделить первое уравнение на второе:
T1/T2=mg/(mg-Fк);
T1/T2=1/(1/4)=4;
4=mg/(mg-Fк);
4(mg-Fк)=mg;
4mg-mg=4Fк;
3mg=4Fк; (уравнение 3).
Т.к. Fк=k*(q1q2/r^2); Подставим эту формулу в уравнение 3:
Так, вот и до второй задачи добрался:
Дано:
m=9,8г=0,0098 кг.
q=1мкКл=1*10^-6 Кл.
T2=T1/4.
r=?
Представим шар, который висит на нити, на него действует сила тяжести mg, которая направлена вниз, и сила натяжения нити T, направленная вверх. Запишем это в формулу:
T1=mg;( Уравнение 1).
Когда же поднесли второй шарик, то на первый уже действует 3 силы:
Сила натяжения нити, сила тяжести и Кулонова сила (Fк). Тогда уравнение примет вид:
T2=mg-Fк.(Уравнение 2).
Т.к. известно, что T2=T1/4, мы можем поделить первое уравнение на второе:
T1/T2=mg/(mg-Fк);
T1/T2=1/(1/4)=4;
4=mg/(mg-Fк);
4(mg-Fк)=mg;
4mg-mg=4Fк;
3mg=4Fк; (уравнение 3).
Т.к. Fк=k*(q1q2/r^2); Подставим эту формулу в уравнение 3:
3mg=4*(k(q1q2/r^2));
3mg*r^2=4*k*q1q2;
r=√((4kq1q2/3mg))=√((4*9*10^9*1*10^-6*1*10^-6)/(3*0,0098*9,8))=0,35(м).
Ускорение свободного падения (g) в этой задаче целесообразно не округлять до 10.
ответ: 0,35 (м).
Согласно II закону Ньютона ma=mg_{1}[/tex], где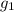 - ускорение свободного падения на той высоте, где летит спутник.
- ускорение свободного падения на той высоте, где летит спутник.
Спутник двигается по окружности под действием только силы тяжести, поэтому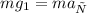
Откуда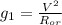
С другой стороны, сила тяжести - это сила всемирного тяготения, поэтому справедливо следующее: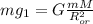 , где M - масса планеты, G - гравитационная постоянная.
, где M - масса планеты, G - гравитационная постоянная.
Отсюда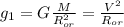
Отсюда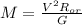
Теперь запишем то же самое для поверхности планеты: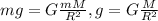 , g - ускорение свободного падения у поверхности планеты (заданное в условии), R - радиус планеты.
, g - ускорение свободного падения у поверхности планеты (заданное в условии), R - радиус планеты.
Подставим в последнее уравнение массу планеты М и получим: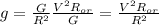
И отсюда находим R: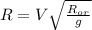
R=3 400 000 м=3 400 км