6. У скільки разів релятивістська маса протона, що має кінетичну енергію 100MeB, більше маси протона, що знаходиться у спокою. Швидкість світла дорівнює 3•108 м/с
Абсолютное значение напряженностей полей E1 и E2, создаваемых соответственно зарядами q1 и q2, в точке A (смотрите схему к решению), лежащей посередине между зарядами, можно найти по формуле:
E1=kq1r2E2=k|q2|r2
Здесь k – коэффициент пропорциональности (из закона Кулона), равный 9·109 Н·м2/Кл2.
По условию точка A посередине между зарядами q1 и q2 (то есть r=l2). Учитывая это, и раскрывая модуль в нижней формуле, получим:
E1=4kq1l2E2=–4kq2l2
На схеме видно, что напряженности E1 и E2 – сонаправлены, поэтому искомую суммарную напряженность E можно найти по формуле:
Если решать эту задачу по школьному, без привлечения инструментария матанализа, то рассуждать можно следующим образом, - в любой точке траектории ускорение свободного падения может быть разложено на две составляющих - вдоль касательной к траектории (нормальное ускорение) и вдоль нормали к траектории (центростремительное ускорение), нам нужна вторая величина, так как она позволяет рассчитать искомый радиус. В наивысшей точке подъема мяча, очевидно, что центростремительное ускорение целиком совпадает с ускорением свободного падения:
Откуда:
Горизонтальная составляющая скорости будет везде одинакова и равна (учтем что 54 км/ч=15 м/с):
Дано:
q1=4 нКл, q2=−2 нКл, l=60 см, r=l2, E−?
Решение задачи:
Абсолютное значение напряженностей полей E1 и E2, создаваемых соответственно зарядами q1 и q2, в точке A (смотрите схему к решению), лежащей посередине между зарядами, можно найти по формуле:
E1=kq1r2E2=k|q2|r2
Здесь k – коэффициент пропорциональности (из закона Кулона), равный 9·109 Н·м2/Кл2.
По условию точка A посередине между зарядами q1 и q2 (то есть r=l2). Учитывая это, и раскрывая модуль в нижней формуле, получим:
E1=4kq1l2E2=–4kq2l2
На схеме видно, что напряженности E1 и E2 – сонаправлены, поэтому искомую суммарную напряженность E можно найти по формуле:
E=E1+E2
Тогда:
E=4kq1l2+–4kq2l2
E=4kl2(q1–q2)
Произвёдем вычисления:
E=4⋅9⋅1090,62(4⋅10–9–(–2⋅10–9))=600В/м
ответ: 600 В/м.
11,25 м
Объяснение:
Если решать эту задачу по школьному, без привлечения инструментария матанализа, то рассуждать можно следующим образом, - в любой точке траектории ускорение свободного падения может быть разложено на две составляющих - вдоль касательной к траектории (нормальное ускорение) и вдоль нормали к траектории (центростремительное ускорение), нам нужна вторая величина, так как она позволяет рассчитать искомый радиус. В наивысшей точке подъема мяча, очевидно, что центростремительное ускорение целиком совпадает с ускорением свободного падения:
Откуда:
Горизонтальная составляющая скорости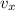
будет везде одинакова и равна (учтем что 54 км/ч=15 м/с):
Искомый радиус кривизны траектории: