ответ:Для расчета значения площади сечения указанной манганиновой проволоки необходимо использовать равенство: U / I = R = ρм * l / S, откуда выразим: S = ρм * l * I / U.Переменные и постоянные: ρм — удельное электрическое сопротивление манганина (по условию ρм = 0,43 Ом*мм2/м); l — длина проволоки (l = 6 м); I — ток (I = 400 мА = 0,4 А); U — действующее напряжение (U = 1,5 В).Вычисление: S = ρм * l * I / U = 0,43 * 6 * 0,4 / 1,5 = 0,688 мм2.ответ: Площадь сечения указанной манганиновой проволоки равна 0,688 мм2.
По закону всемирного тяготения сила взаимодействия
1) , где — масса Земли, — масса Луны, — радиус орбиты Луны.
С другой стороны, Луна движется только с центростремительным ускорением, значит по II закону Ньютона
2) , где — центростремительное ускорение;
3) , где — угловая скорость;
4) , где — период обращения Луны вокруг Земли;
5)
6)
Тогда
7)
8)
К слову, масса Земли, которая фигурирует в последней формуле, была вычислена в 1798 году Генри Кавендишем на основе уже известного в то время радиуса Земли. Радиус же Земли был вычислен опытным путём в 240 году до нашей эры Эратосфеном Киренским. Поэтому предлагаю перейти в нашей формуле от массы Земли к радиусу Земли. Мы знаем, что тело на поверхности Земли движется с ускорением , и на основе вышеизложенного можем написать аналогичное уравнение
ответ:Для расчета значения площади сечения указанной манганиновой проволоки необходимо использовать равенство: U / I = R = ρм * l / S, откуда выразим: S = ρм * l * I / U.Переменные и постоянные: ρм — удельное электрическое сопротивление манганина (по условию ρм = 0,43 Ом*мм2/м); l — длина проволоки (l = 6 м); I — ток (I = 400 мА = 0,4 А); U — действующее напряжение (U = 1,5 В).Вычисление: S = ρм * l * I / U = 0,43 * 6 * 0,4 / 1,5 = 0,688 мм2.ответ: Площадь сечения указанной манганиновой проволоки равна 0,688 мм2.
Объяснение:
По закону всемирного тяготения сила взаимодействия
1)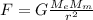 , где
, где 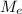 — масса Земли,
— масса Земли, 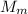 — масса Луны,
— масса Луны,  — радиус орбиты Луны.
— радиус орбиты Луны.
С другой стороны, Луна движется только с центростремительным ускорением, значит по II закону Ньютона
2)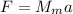 , где
, где  — центростремительное ускорение;
— центростремительное ускорение;
3)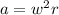 , где
, где 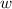 — угловая скорость;
— угловая скорость;
4)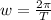 , где
, где 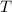 — период обращения Луны вокруг Земли;
— период обращения Луны вокруг Земли;
5)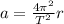
6)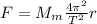
Тогда
7)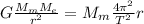
8)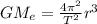
К слову, масса Земли, которая фигурирует в последней формуле, была вычислена в 1798 году Генри Кавендишем на основе уже известного в то время радиуса Земли. Радиус же Земли был вычислен опытным путём в 240 году до нашей эры Эратосфеном Киренским. Поэтому предлагаю перейти в нашей формуле от массы Земли к радиусу Земли. Мы знаем, что тело на поверхности Земли движется с ускорением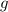 , и на основе вышеизложенного можем написать аналогичное уравнение
, и на основе вышеизложенного можем написать аналогичное уравнение
9)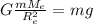 , где
, где 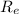 — радиус Земли;
— радиус Земли;
10)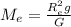
Подставим массу Земли в формулу 8.