Напомню, что функция от одной переменной, говоря вне рамок каких-либо алгебраических теорий, есть некоторый закон, находящий своё отражение в неком алгебраическом выражении, который ставит в однозначное соответствие каждому элементу x, принадлежащему множеству X(; притом множество X в данном случае называют множеством определения этой функции, а элемент этого множества - аргументом) каждый элемент (Y - множество значений, а его элемент, соответствующий определённому значению мн. X - значение функции в этой точке). Функции такого рода могут являться математическими моделями очень большого спектра реальных ситуаций: например, ваша позиция в очереди за хлебом с x количеством человек будет задаваться функцией . Геометрической моделью функции от одной переменной является график функции. Его интуитивно можно определить, как некоторое множество точек на плоскости с заданными декартовыми координатами, координаты каждой из которых связаны математическим выражением, задающим функцию. Например, графиком функции прямая, не проходящая через начало координат, возрастающая.
Помните вдальнейшем, что функцию от одной переменной в математике принято обозначать следующим образом: на примере вашей функции (читается: "эф от икс"), где или просто .
Для того, чтобы ответить на вопрос об области определения функции, нужно преобразовать подкоренное выражение в правой части.
.
Напомню, что в область определения функци от одной переменной входят все допустимые значения, т.е. значения, при которых выражение имеет смысл.
Выражение имеет смысл при (т.к. квадратный корень нельзя изелекать из отрицательного числа)
у = √(2 + 9х - 5х²)
Подкоренное выражение не может быть отрицательным
2 + 9х - 5х² ≥ 0
Найдём нули функции 2 + 9х - 5х²
- 5х²+ 9х + 2 = 0
D = 81 + 40 = 121
√D = 11
x₁ = (-9 - 11):(-10) = 2
x₁ = (-9 + 11):(-10) = -0,2
Поскольку график функции 2 + 9х - 5х² - квадратная парабола веточками вниз, то неравенство верно при
х∈ [-0,2; 2]
Область определения D(y) = [-0,2; 2]
Напомню, что функция от одной переменной, говоря вне рамок каких-либо алгебраических теорий, есть некоторый закон, находящий своё отражение в неком алгебраическом выражении, который ставит в однозначное соответствие каждому элементу x, принадлежащему множеству X(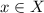 ; притом множество X в данном случае называют множеством определения этой функции, а элемент этого множества - аргументом) каждый элемент
; притом множество X в данном случае называют множеством определения этой функции, а элемент этого множества - аргументом) каждый элемент 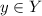 (Y - множество значений, а его элемент, соответствующий определённому значению мн. X - значение функции в этой точке). Функции такого рода могут являться математическими моделями очень большого спектра реальных ситуаций: например, ваша позиция в очереди за хлебом с x количеством человек будет задаваться функцией
(Y - множество значений, а его элемент, соответствующий определённому значению мн. X - значение функции в этой точке). Функции такого рода могут являться математическими моделями очень большого спектра реальных ситуаций: например, ваша позиция в очереди за хлебом с x количеством человек будет задаваться функцией 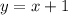 . Геометрической моделью функции от одной переменной является график функции. Его интуитивно можно определить, как некоторое множество точек на плоскости с заданными декартовыми координатами, координаты каждой из которых связаны математическим выражением, задающим функцию. Например, графиком функции
. Геометрической моделью функции от одной переменной является график функции. Его интуитивно можно определить, как некоторое множество точек на плоскости с заданными декартовыми координатами, координаты каждой из которых связаны математическим выражением, задающим функцию. Например, графиком функции 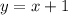 прямая, не проходящая через начало координат, возрастающая.
прямая, не проходящая через начало координат, возрастающая.
Помните вдальнейшем, что функцию от одной переменной в математике принято обозначать следующим образом: на примере вашей функции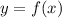 (читается: "эф от икс"), где
(читается: "эф от икс"), где  или просто
или просто 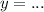 .
.
Для того, чтобы ответить на вопрос об области определения функции, нужно преобразовать подкоренное выражение в правой части.
Напомню, что в область определения функци от одной переменной входят все допустимые значения, т.е. значения, при которых выражение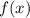 имеет смысл.
имеет смысл.
Выражение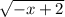 имеет смысл при (т.к. квадратный корень нельзя изелекать из отрицательного числа)
имеет смысл при (т.к. квадратный корень нельзя изелекать из отрицательного числа)
ответ: область определения - луч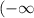 ; 2].
; 2].