1+sin2x-sinx=cosx
cos^2(x)+sin^2(x)+2sinxcosx-sinx-cosx=0
(sinx+cosx)^2-(sinx+cosx)=0
(sinx+cosx)(sinx+cosx-1)=0
sinx+cosx=0|:cosx не равный 0 или sinx+cosx-1=0
tgx+1=0 sinx+cosx=1
tgx=-1 sqrt{2}cos(П/4-x)=1
x=-П/4+Пn, n принадлежит N cos(П/4-x)=1/sqrt{2}
cos(П/4-x)=sqrt[2}/2
П/4-x=(+-)П/4+2Пn, n N
-x=(+-)П/4-П/4+2Пn, n N
x=(-+)П/4+П/4-2Пn, n N
Воспользуемся основным тригон. тождеством и формулой синуса двойного угла, чтобы разложить на множители:
Отсюда имеем два уравнения:
sinx+cosx = 0 и sinx+cosx = 1
tgx = -1 √2*sin(x+π/4)=1
x = -π/4 + πk sin(x+π/4)= 1/√2
ответ: -π/4 + πk; ; K,n∈Z
1+sin2x-sinx=cosx
cos^2(x)+sin^2(x)+2sinxcosx-sinx-cosx=0
(sinx+cosx)^2-(sinx+cosx)=0
(sinx+cosx)(sinx+cosx-1)=0
sinx+cosx=0|:cosx не равный 0 или sinx+cosx-1=0
tgx+1=0 sinx+cosx=1
tgx=-1 sqrt{2}cos(П/4-x)=1
x=-П/4+Пn, n принадлежит N cos(П/4-x)=1/sqrt{2}
cos(П/4-x)=sqrt[2}/2
П/4-x=(+-)П/4+2Пn, n N
-x=(+-)П/4-П/4+2Пn, n N
x=(-+)П/4+П/4-2Пn, n N
Воспользуемся основным тригон. тождеством и формулой синуса двойного угла, чтобы разложить на множители:
1+sin2x-sinx=cosx
Отсюда имеем два уравнения:
sinx+cosx = 0 и sinx+cosx = 1
tgx = -1 √2*sin(x+π/4)=1
x = -π/4 + πk sin(x+π/4)= 1/√2
ответ: -π/4 + πk;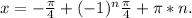 ; K,n∈Z
; K,n∈Z