Знайдіть площу фігури, обмеженої параболою y=х^2 та прямими у=0; х=2.

Показать ответ

Ответ:

lisska2

19.03.2023 01:05

X^2 - xy + y^2 = 3 |*5 2x^2 - xy - y^2 = 5 |*3 5x^2 - 5xy + 5y^2 = 15 6x^2 - 3xy - 3y^2 = 15 |(2)-(1) x^2 + 2xy - 8y^2 = 0 Подставляя значение х = 0 и y = 0 в исходную систему, убеждаемся, что (0; 0) не является её решением. Поэтому можем почтенно разделить полученное уравнение на xy. x/y + 2 - 8y/x = 0 Замена x/y = t, t <> 0 t + 2 - 8/t = 0 | *t t^2 + 2t - 8 = 0 По теореме Виета: t1 = -4, t2 = 2. При t = -4: x/y = -4 или x = -4y. Подставляем в первое уравнение исходной системы: (-4y)^2 - (-4y)*y + y^2 = 3 21y^2 = 3 y = (+/-) 1/sqrt7 x = (-/+) 4/sqrt7 При t = 2: x/y = 2 или x = 2y. Подставляем в первое уравнение исходной системы: (2y)^2 - 2y*y + y^2 = 3 3y^2 = 3 y = (+/-) 1 x = (+/-) 2 ответ: (1/sqrt7; -4/sqrt7), (-1/sqrt7; 4/sqrt7), (1; 2), (-1; -2).

Объяснение:

0,0(0 оценок)

Ответ:

NikuSonada

09.08.2021 12:48

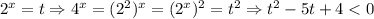
1. Пусть $2^x=t \Rightarrow 4^x=(2^2)^x=(2^x)^2=t^2 \Rightarrow t^2-5t+4$

Решать надо методом интервалов, для этого надо найти нули функции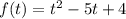 f(t)=t^2-5t+4 , решим для уравнение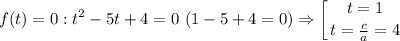 $\displaystyle f(t) = 0: t^2-5t+4=0 \ (1-5+4=0) \Rightarrow \left [ {{t=1} \atop {t=\frac{c}{a}=4 }} \right.$

Получаем разложение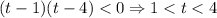 (t-1)(t-4)

Там интервалы были, знаки на них +-+, выбрали средний

Возвращаемся к замене

Такой переход имели право сделать, так как функция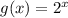 g(x)=2^x - монотонно возрастающая функция.

2. y=5-x^2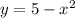 - парабола с ветвями, направленными вниз, 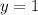y=1 - просто прямая и фигура, образованная при их пересечении будет такова, что кусок параболы будет лежать выше.

Вспомним, что для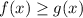 $f(x)\geq g(x)$ на некотором интервале, то площадь фигуры будет равна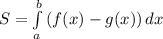 $S = \int\limits^b_a {(f(x)-g(x))} \, dx$

В нашем случае нужно вычислить пределы, а это как раз абсциссы точек пересечения, то есть нужно решить уравнение

$5-x^2=1 \Rightarrow x^2=4 \Rightarrow x=\pm2$ , пределы нашли, вычисляем:

$\displaystyle S = \int\limits^2_{-2} {(5-x^2-1)} \, dx = \int\limits^2_{-2} {(4-x^2)} \, dx = \bigg(4x-\frac{x^3}{3}\bigg) \bigg|\limits_{-2}^2 = \\=4\cdot 2-\frac{2^3}{3}-\bigg(4\cdot(-2) - \frac{(-2)^3}{3} \bigg) =8+8-\frac{8}{3}-\frac{8}{3}=16-\frac{16}{3}=\\=\frac{48-16}{3}=\frac{32}{3}=10\frac{2}{3}$