Разберем последовательно как можно просто и без ошибок построить график любой функции.
Для этого первым делом рассмотрим функцию, график которой нужно построить.
Данная функция представлена в виде дроби целого известного числа и неизвестного, причем неизвестное стоит в знаменателе дроби. Вспоминаем математику начальных классов, когда учили, что делить нельзя только на ноль. Из этого делаем вывод, что неизвестное число х для заданной функции может быть каким угодно, кроме нуля. Теперь можно записать область значений переменной х:
Проверим, является ли функция четной. Для этого подставим —х в ее уравнение вместо х и сделаем вывод:
Получаем нечетную функцию. Для нас такая информация полезна тем, что график нечетной функции симметричен началу координат, то есть точке (0; 0).
Найдем точки, которые принадлежат графику, чтобы провести через них кривую. Выберем точки произвольно и подставим вместо х:
Примем за 1 - объем цистерны
Пусть t цис./ч - производительность "медленного" насоса.
Тогда 3t цис./ч - производительность "быстрого" насоса.
(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.
(t+3t)
- объем работы системы из двух насосов за 2ч 15мин.
Получим уравнение:
9t = 1
Значит,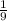
- цис./ч - производительность "медленного" насоса.
Тогда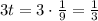
- цис./ч - производительность "быстрого" насоса.
Следовательно,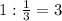
ч - потребуется "быстрому" насосу на заполнение цистерны.
ответ: 3 ч.
Объяснение:
Решение.
Разберем последовательно как можно просто и без ошибок построить график любой функции.
Для этого первым делом рассмотрим функцию, график которой нужно построить.
Данная функция представлена в виде дроби целого известного числа и неизвестного, причем неизвестное стоит в знаменателе дроби. Вспоминаем математику начальных классов, когда учили, что делить нельзя только на ноль. Из этого делаем вывод, что неизвестное число х для заданной функции может быть каким угодно, кроме нуля. Теперь можно записать область значений переменной х:
Проверим, является ли функция четной. Для этого подставим —х в ее уравнение вместо х и сделаем вывод:
Получаем нечетную функцию. Для нас такая информация полезна тем, что график нечетной функции симметричен началу координат, то есть точке (0; 0).
Найдем точки, которые принадлежат графику, чтобы провести через них кривую. Выберем точки произвольно и подставим вместо х: