Здравствуйте с заданием по алгебре дам 25 б Контрольная работа №3 « Линейная функция»

1.Функция задана формулой у =1/2х=7 найдите:

а)значение функции, соответствующее значению аргумента,

равному 4; ( х = 4 )

б) значение аргумента, при котором значение функции

равно –8. (у = -8 )

2.а)Постройте график функции у = 3х – 4.

б) С графика найдите значение функции,

соответствующее значению аргумента 2,5.

3.В одной системе координат постройте графики функций:

а) у = –0,5х; б) у = 2.

4.Проходит ли график функции у = –5х + 11 через точку:

а) М(6; –41); б) N(–5; 36) ?

5. Каково взаимное расположение графиков функций

у = 15х – 51 и у = –15х + 39? В случае пересечения графиков

найдите координаты точки их пересечения.

Показать ответ

Ответ:

яяя489

19.02.2022 02:42

Для решения запишем формулу бинома Ньютона:

$(a+b)^n=a^n+C_n^1a^{n-1}b+C_n^2a^{n-2}b^2+...+b^n$

Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение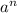 a^n .

Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение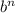 b^n .

Рассмотрим многочлен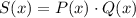 $S(x)=P(x)\cdot Q(x)$ , где:

$P(x)=(3x^7+6x^4-1)^{12}$

Q(x)=(5x^2+2)^3

Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.

Для многочлена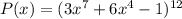 $P(x)=(3x^7+6x^4-1)^{12}$ :

- степень определяется выражением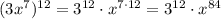 $(3x^7)^{12}=3^{12}\cdot x^{7\cdot12}=3^{12}\cdot x^{84}$ , то есть степень равна 84

- свободный член равен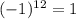 $(-1)^{12}=1$

Для многочлена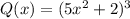 Q(x)=(5x^2+2)^3 :

- степень определяется выражением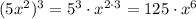 $(5x^2)^3=5^3\cdot x^{2\cdot3}=125\cdot x^6$ , то есть степень равна 6

- свободный член равен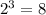 2^3=8

Наконец, для многочлена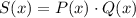 $S(x)=P(x)\cdot Q(x)$ получим:

- степень определяется выражением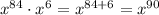 $x^{84}\cdot x^6=x^{84+6}=x^{90}$ , то есть степень равна 90

- свободный член равен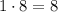 $1\cdot8=8$

Сумма степени и свободного члена многочлена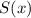 S(x) :

90+8=98

ответ: 98

0,0(0 оценок)

Ответ:

Kaytha

22.05.2023 20:08

Координаты точки пересечения прямых (2; 4)

Решение системы уравнений (2; 4).

Объяснение:

Решить систему уравнений графическим

3x-y=2

x+2y=10

Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.

Прежде преобразуем уравнения в более удобный для вычислений вид:

3x-y=2 x+2y=10

-у=2-3х 2у=10-х

у=3х-2 у=(10-х)/2

Таблицы:

х -1 0 1 х -2 0 2

у -5 -2 1 у 6 5 4

Согласно графика, координаты точки пересечения прямых (2; 4)

Решение системы уравнений (2; 4).

0,0(0 оценок)

Популярные вопросы: Алгебра