Запишіть у вигляді виразу: 1) число, протилежне числу a;
2) число, обернене до числа а;
3) суму чисел x і y;
4) число, обернене до суми чисел x і y;
5) суму чисел, обернених до чисел x і y;
6) суму числа a та його квадрата;
7) частку від ділення числа a на число, протилежне числу b;
8) добуток суми чисел a і b та числа, оберненого до числа c;
9) різницю добутку чисел m і n та частки чисел p і q;

Показать ответ

Ответ:

marina200810

13.01.2022 21:08

На выполнение заказа потребовалось 7 дней

Объяснение:

Производительность первой бригады составляет 3 единицы в день.

Производительность второй бригады составляет 9 единицы в день.

К концу 4- го дня, объем работы выполненный первой бригадой оценивается в 12 единиц, а второй в 36 единиц. Разница составила 24 единицы.

Начиная с пятого дня, производительность первой бригады составляет уже 10 единиц в день, а второй 2 единицы в день.

С этого момента представим график, где оси X соответствует количество дней, а оси Y объем выполненной работы, начиная с пятого дня. График первой бригады начинается в точке (0;0) и каждое последующее значение у больше значения x в 10 раз. График второй бригады начинается в точке (0;24) и каждое последующее значение у больше значения x в 2 раза.

В виде системы линейных уравнений это будет выглядеть следующим образом:

y=2x+24

y=10x

10x=2x+24

8x=24

x=3

То есть через три дня обе бригады одновременно достигнут равного объема выполненной работы.

Итого: 4+3=7 дней.

0,0(0 оценок)

Ответ:

supermichail29

25.08.2021 13:59

Выделим полный квадрат.

$y=-2x^2+5x+3;y=-2(x^2-2*5x/4+(5/4)^2-(5/4)^2)+3\\y=-2(x-5/4)^2-(-2*25/16)+3\\y=-2(x-1.25)^2+49/8\\y=-2(x-1.25)^2+6.125$

Найдём нули этой функции.

$(x-5/4)^2=49/16\\x-5/4=б7/4\\x_1=12/4=3;x_2=2/4=0.5$

Найдём точку пересечения с осью Оу.

y(0)=-2*0^2+5*0+3=3

Как я буду строить: я буду последовательно изменять функции

1. Есть функция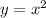 y=x^2 как она выглядит известно.

2. Функция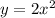 y=2x^2 чуть уже, она сжата к оси Оу.

3.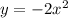 y=-2x^2 перевёрнута вниз (развернули на 180°).

4.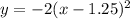 y=-2(x-1.25)^2 график сдвинут вправо на 1.25.

5. y=-2(x-1.25)^2+6.125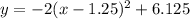 график подняли вверх на 6.125.

Получили график нашей функции.

Точки пересечения с осями мы уже знаем, и исходя из переноса функции, можно понять какой будет координата вершины параболы.

Конечно обычно сразу отмечают координаты вершины и соединяют её с нулями функции, просто хотел объяснить по какому принципу строятся функции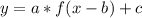 y=a*f(x-b)+c когда известно как выглядит y=f(x).