Із двоих міст, відстань між яркими дорівнює 280 км, одночасно назустріч один одному виїхали два автомобілі, і зустрілися через 2 години. Відомо, шо до моменту зустрічі один з автомобілів проїхав на 40 км больше, ніж інший. Знайдіть швидкість автомобілів
Нужно составить систему линейных уравнений
4. Скорость второго грузовика 510 км/ч.
5. 0; -1.
Объяснение:
В задаче требуется найти скорость второго грузовика.
4. Решить задачу.
Расстояние - 510 км;
Скорость первого грузовика - ?, на 10км/ч больше второго;
Скорость второго грузовика - ?
Время первого грузовика - ? , на 1 час 42 мин меньше второго.
Вспомним формулы расстояния и времени:
Переведем минуты в часы.
1 час = 60 мин ⇒ 1 мин = 1/60 час
42 мин равны:
1 ч 42 мин = 1 ч + 42 мин =1 ч + 7/10 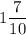ч =
ч
Пусть скорость второго грузовика равна х км/ч, тогда скорость первого грузовика равна (х+10) км/ч.
Расстояние равно 510 км.
Тогда время второго грузовика:
Время первого грузовика:
Время второго на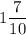
ч больше первого.
Составим уравнение:
х₂ - посторонний корень, так как скорость не может быть отрицательной.
Скорость второго грузовика 510 км/ч.
5. Решить уравнение:
(2m-1)² = -3-4·(2m-1)
Квадрат разности двух чисел равен: (a + b)² = a² + 2ab +b².Раскроем скобки:
4m² - 4m + 1=-3 - 8m + 4
Перенесем все слагаемые из правой части в левую часть, не забывая поменять знак на противоположный:
4m² - 4m + 1 + 3 + 8m -4=0
Приведем подобные члены и вынесем общий множитель:
4m² + 4m = 0
4m(m+1) = 0
Произведение равно нулю, если хотя бы один из сомножителей равен нулю.4m = 0 или m + 1 = 0
m = 0 или m = -1
ответ: 0; -1
найду координаты точки пересечения диагоналей О-это середина АС
координата х : (-2+4)/2=1
y: (-4+2)/2=-1
z: (5+(-3))/2=1
O(1;-1;1)
пусть координаты четвертой вершины параллелограмма D (x;y;z)
тогда О-середина BD
распишу координаты О через B и D
по х: 1=(-1+x)/2; -1+x=2; x=3
y: -1=(4+y)/2; 4+y=-2;y=-6
z: 1=(2+z)/2; 2+z=2;z=0
D(3;-6;0)
Теперь осталось найти cos<AOB в треугольнике АОВ по т косинусов, предварительно посчитав его стороны
AO²=(1-(-2))²+(-1+(-4))²+(1-5)²=9+25+16=50; AO=5√2
AB²=(-1+2)²+(4+4)²+(2-5)²=1+64+9=74; AB=√74
BO²=(1+1)²+(-1-4)²+(1-2)²=4+25+1=30; BO=√30
тогда по т косинусов
AB²=AO²+AB²-2*AO*BO*cos<AOB
74=50+30-2*5√2*√30*cos<AOB
cos<AOB=6/(10√60)≈0.077-почти прямой угол