Як вказати область значень і проміжки зростання та спадання функції

Показать ответ

Ответ:

LizaVeta281

23.02.2020 13:55

$\boxed{\dfrac{8}{3}}$ квадратных единиц

Объяснение:

Построим график $y = -x^{2} + 4x - 4$

Пусть S площадь ограниченная графиком функции $y = -x^{2} + 4x - 4$ осями координат. Пусть точка B - пересечение графика y и оси абсцисс, точка A - пересечение графика y и оси ординат.

$y(0) = -0^{2} + 4 * 0 - 4 = -4$

y = 0

$-x^{2} + 4x - 4 = 0|*(-1)$

$x^{2} - 4x + 4 =0$

$(x - 2)^{2} = 0 \Longleftrightarrow x - 2 =0$

x = 2

Координаты точек A и B:

A(0;-4)

B(2;0)

Пусть точка начало системы координат, тогда точка O имеет координаты O(0;0).

Узнаем уравнение прямой проходящей через точки A и B. Уравнение прямой с угловым коэффициентом в общем виде: y = kx + b .

$\displaystyle \left \{ {{A: -4=k * 0 + b} \atop {B:0=2*k + b}} \right.$ $\displaystyle \left \{ {{ b=-4} \atop {0=2k - 4}} \right.$ $\displaystyle \left \{ {{ b=-4} \atop {4=2k |:2}} \right.$ $\displaystyle \left \{ {{ b=-4} \atop {k = 2}} \right.$

y = 2x - 4

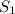Пусть $S_{1}$ - площадь между прямой 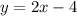y = 2x - 4 и функцией $y = -x^{2} + 4x - 4$

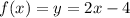Пусть f(x) = y = 2x - 4 и $g(x) = y = -x^{2} + 4x - 4$ .

$S = S_{\bigtriangleup AOB} - S_{1}$

$OA = \sqrt{(x_{A} - x_{O})^{2} + (y_{A} - y_{O})^{2}} = \sqrt{(0 - 0)^{2} + (-4 - 0)^{2}} =\sqrt{16} = 4$

$OB = \sqrt{(x_{B} - x_{O})^{2} + (y_{B} - y_{O})^{2}} = \sqrt{(2 - 0)^{2} + (0 - 0)^{2}} =\sqrt{4} = 2$

По формуле площади прямоугольного треугольника:

$S_{\bigtriangleup AOB} = \dfrac{AO * OB}{2} = \dfrac{4 * 2}{2} = 4$ .

Промежуток интегрирования: [0;2]

Докажем, что $f(x) \geq g(x)$ при $x \in [0;2]$

$2x- 4 \geq -x^{2} + 4x - 4$

$x^{2} - 2x \geq 0$

$x(x - 2) \geq 0$

$x \in (-\infty;0] \cup [2;+\infty)$ тогда можно сделать вывод, что

$g(x) \geq f(x)$ при $x \in [0;2]$ .

По теореме:

$S_{1} = \displaystyle \int\limits^2_0 {(g(x) - f(x))} \, dx = \int\limits^2_0 {-x^{2} +4x - 4 - 2x + 4} \, dx = \int\limits^2_0 {2x-x^{2}} \, dx =$

$= x^{2} - \dfrac{x^{3} }{3} \bigg|_0^2 = (2^{2} - \dfrac{2^{3} }{3}) - 0 = 4 - \dfrac{8}{3} = \dfrac{12 - 8}{3} = \dfrac{4}{3}$ .

$S = S_{\bigtriangleup AOB} - S_{1} = 4 - \dfrac{4}{3} = \dfrac{12 -4}{3} = \dfrac{8}{3}$ квадратных единиц.

найти площадь фигуры,ограниченной осями координат и параболой

0,0(0 оценок)

Ответ:

anastasiagarap

18.01.2021 17:06

Объяснение:

№89

∠СDA = 90°, т.к. Вписанный угол, опирающийся на диаметр, является прямым углом. Следовательно,

ΔСDA - прямоугольный. Сумма всех углов = 180°. Значит,

∠DAC = 180° - 90° - 54° = 36°

∠ВАD = ∠DAC +∠САВ, откуда

∠САВ = ∠ВАD - ∠DAC = 78°-36° =42°

∠САВ = 42°

№ 90

1) Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами, т.е.

∠α = ½ ∪АВ, откуда

∪АВ = 2∠∝

α = 40° → β = 80° (1а ) → α + β =120° (1с )

α = 70° → β = 140° (2с) α + β =210°

α = 80° → β = 160° (3d) α + β = 240° (3b)

ответ: 1а, 1 с

2с

3d, 3b

0,0(0 оценок)

Популярные вопросы: Алгебра