Оба этих уравнения являются уравнениями окружности.
Общее уравнение окружности:
где -координаты вершины окружности, R-радиус
a)
(-2;-4)-вершина, R=6
В системе координат отмечаем точку с координатами (-2;-4) и чертим окружность с центром в этой точке радиусом равным 6. Это и есть график нашей функции.(Совет-выбрать единичный отрезок равный 1 клеточке тетради)
б)[ tex]x^{2}+(y-1)^{2}=2,25[/tex]
(0;1)-вершина, R=1,5
В системе координат отмечаем точку с координатами (0;1)) и чертим окружность с центром в этой точке радиусом равным 1,5. Это и есть график нашей функции.(Совет-выбрать единичный отрезок равный двум клеточкам тетради)
Найдём скорость (мощность), с которой воду перекачивает каждый насос, для этого кол-во воды разделим на время:
∨₁= 8/5;
∨₂=8/7;
где ∨₁ и ∨₂ скорости первого и второго насоса соответственно.
Найдём суммарную скорость (мощность), с которой оба насоса будут перекачивать воду:
∨₀=∨₁+∨₂=8/5+8/7=96/35;
Теперь, зная скорость и кол-во воды(96, по условию), найдём время:
t=96/∨₀=35.
ответ: Насосы должны работать сообща 35 минут.
Оба этих уравнения являются уравнениями окружности.
Общее уравнение окружности:
где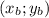 -координаты вершины окружности, R-радиус
-координаты вершины окружности, R-радиус
a)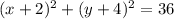
(-2;-4)-вершина, R=6
В системе координат отмечаем точку с координатами (-2;-4) и чертим окружность с центром в этой точке радиусом равным 6. Это и есть график нашей функции.(Совет-выбрать единичный отрезок равный 1 клеточке тетради)
б)[ tex]x^{2}+(y-1)^{2}=2,25[/tex]
(0;1)-вершина, R=1,5
В системе координат отмечаем точку с координатами (0;1)) и чертим окружность с центром в этой точке радиусом равным 1,5. Это и есть график нашей функции.(Совет-выбрать единичный отрезок равный двум клеточкам тетради)