1) х = 0,25
2) х = -5
3) y= -0.6
4) y = -0.75
Объяснение:
1) x(x-4)=2+(x-1)²;
х*х + х*(-4) = 2 + (х-1)(х+1)
- 4х = 2+ х*х + х*1 - 1*х - 1*1
- 4х = 2 + + х - х - 1
-4х - х + х = 2 - 1
-4х = 1
х = 1/4
х = 0,25
2). (x+2)(x-3)-3=(x+1)²
х*х + х*(-3) + 2*х + 2*(-3) = (х+1)(х-1)
- 3х + 2х - 6 = - х + х - 1
-х = 5 (умножить на -1)
х = -5
3)y(5-y)=1-(y+2)²
5у - = 1 - (y+2)(y-2)
5y - = 1 - - 2y + 2y - 4
5y + 2y -2y = 1-4
5y = -3
y = -3/5
y = -0.6
4) (y-1)²-(y+1)(y-7)=0.
(y-1)(y+1) - + 7y + y + 7 = 0
+ y - y - 1 - + 7y + y + 7 = 0
8y = -6
y = -6/8
y = -0.75
1. При p = 0 неравенство теряет главного члена:
px^2 + (2p + 1)x - (2 - p) < 0;
0 * x^2 + (2 * 0 + 1)x - (2 - 0) < 0;
x - 2 < 0;
x < 2;
x ∈ (-∞; 2).
Значение p = 0 не подходит, т. к. не все значения x являются корнями неравенства.
2. При p > 0 ветви параболы направлены вверх, следовательно, не все значения x являются корнями неравенства.
3. При p < 0 неравенство будет верно при всех значениях x, если дискриминант будет отрицательным:
D = b^2 - 4ac;
D = (2p + 1)^2 + 4p(2 - p);
D = 4p^2 + 4p + 4 + 8p - 4p^2;
D = 12p + 4;
D < 0;
12p + 4 < 0;
12p < -4;
p < -4/12;
p < -1/3;
p ∈ (-∞; -1/3).
ответ: при значениях p ∈ (-∞; -1/3).
1) х = 0,25
2) х = -5
3) y= -0.6
4) y = -0.75
Объяснение:
1) x(x-4)=2+(x-1)²;
х*х + х*(-4) = 2 + (х-1)(х+1)
-4х - х + х = 2 - 1
-4х = 1
х = 1/4
х = 0,25
2). (x+2)(x-3)-3=(x+1)²
х*х + х*(-3) + 2*х + 2*(-3) = (х+1)(х-1)
-х = 5 (умножить на -1)
х = -5
3)y(5-y)=1-(y+2)²
5у -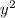 = 1 - (y+2)(y-2)
= 1 - (y+2)(y-2)
5y -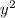 = 1 -
= 1 - 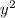 - 2y + 2y - 4
- 2y + 2y - 4
5y + 2y -2y = 1-4
5y = -3
y = -3/5
y = -0.6
4) (y-1)²-(y+1)(y-7)=0.
(y-1)(y+1) -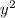 + 7y + y + 7 = 0
+ 7y + y + 7 = 0
8y = -6
y = -6/8
y = -0.75
1. При p = 0 неравенство теряет главного члена:
px^2 + (2p + 1)x - (2 - p) < 0;
0 * x^2 + (2 * 0 + 1)x - (2 - 0) < 0;
x - 2 < 0;
x < 2;
x ∈ (-∞; 2).
Значение p = 0 не подходит, т. к. не все значения x являются корнями неравенства.
2. При p > 0 ветви параболы направлены вверх, следовательно, не все значения x являются корнями неравенства.
3. При p < 0 неравенство будет верно при всех значениях x, если дискриминант будет отрицательным:
D = b^2 - 4ac;
D = (2p + 1)^2 + 4p(2 - p);
D = 4p^2 + 4p + 4 + 8p - 4p^2;
D = 12p + 4;
D < 0;
12p + 4 < 0;
12p < -4;
p < -4/12;
p < -1/3;
p ∈ (-∞; -1/3).
ответ: при значениях p ∈ (-∞; -1/3).