Значение функции может принимать максимальное или минимальное значение в точках касания, когда касательная параллельна оси ОХ, т.е. угловой коэффициент этой прямой равен 0, т.к.tg0=0 значит ], решаем квадратное уравнение:
Корни:x=-20/3=-6,(6), он не подходит т.к. x может принимать значения от -5 до 8,
2-ой корень x=-4, подставим это значение в начальную функцию: и получим y=2, теперь подставим -5 и 8:
Найдем производную функции
Значение функции может принимать максимальное или минимальное значение в точках касания, когда касательная параллельна оси ОХ, т.е. угловой коэффициент этой прямой равен 0, т.к.tg0=0 значит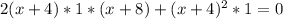 ], решаем квадратное уравнение:
], решаем квадратное уравнение:
Корни:x=-20/3=-6,(6), он не подходит т.к. x может принимать значения от -5 до 8,
2-ой корень x=-4, подставим это значение в начальную функцию: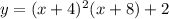 и получим y=2, теперь подставим -5 и 8:
и получим y=2, теперь подставим -5 и 8:
x=-5,y=5
x=8,y=2306, т.е. наименьшее значение функции y=2
ответ: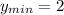
И график в доказательство
а) -7х+5(2х-3)=6
-7х+10х-75=6
3х=6+75
х=81:3
х=27
б)5х-7(3-х)=2х+11
5х-21+7х=2х+11
5х+7х-2х=11+21
10х=32
х=3,2
в)0,3-2(х+1)=0,4х+0,1
0,3-2х-2=0,4х+0,1
-2х-0,4х=0,1-0,3+2
-2,4х=1,8
х=1,8:(-2,4)
х=-0,75
г)6х-3,2=7х-3(2х-2,5)
6х-3,2=7х-6х+7,5
6х-7х+6х=7,5+3,2
5х=10,7
х=2,14
№ 758
а)(х-2)(х-3)=х(х+1)
x^-3x-2x+6=x^+x
x^-3x-2x-x^-x=-6
-6x=-6
x=1
б)(х+4)(х+6)-х^=30
x^+6x+4x+24-x^=30
10x=6
x=0.6
в)(х-5)(х+1)=х^+5
x^+x-5x-5=x^+5
x^+x-5x-x^=5+5
-4x=10
x=-2.5
г)(х-1)(х-3)=(х-2)(х-4)
x^-3x-x+3=x^-4x-2x+8
x^-3x+x-x^+4x+2x=8-3
4x=5
x=1.25