f'(x)=ln(cos3x)=(3x)'*(cos3x)'*(lncos3x)'=3*(-sin3x)*(1/cos3x)=-3sin3x/cos3x=-3tg3x
при х=п/9, f'(x)=f'(п/9)=-3(tg(п/3))=-3*корень квадратный из 3
f'(x)=
f'(П/9)=-3*tgП/3=-3√3
f'(x)=ln(cos3x)=(3x)'*(cos3x)'*(lncos3x)'=3*(-sin3x)*(1/cos3x)=-3sin3x/cos3x=-3tg3x
при х=п/9, f'(x)=f'(п/9)=-3(tg(п/3))=-3*корень квадратный из 3
f'(x)=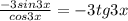
f'(П/9)=-3*tgП/3=-3√3