Вычислите (cos (5x + 1)) ' Выберите один ответ:
1. 5sin x
2. 5cos (x + 1)
3. – 5sin (5x + 1)

Показать ответ

Ответ:

kakniet

18.04.2021 08:48

25 (км/ч)

Объяснение:

Расстояние против течения - Sпр.теч. = 100 км

Время против течения - tпр.теч. = 4часа

Расстояние по течению - Sпо теч. = 150 км

Время по течению - tпо теч. = 5 часов

На сколько км/ч скорость течения реки меньше собственной скорости лодки?

Пусть Vc. - собственная скорость лодки, а Vт. - скорость течения реки.

⇒ Vпо теч.=Vс. + Vт., Vпр.теч. = Vс. - Vт.

Чтобы найти скорость, нужно расстояние разделить на время:

$\displaystyle V=\frac{S}{t}$

Найдем скорости по течению и против течения:

Vпр.теч. = 100:4 = 25 (км/ч)

Vпо теч. = 150:5 = 30 (км/ч)

Получим систему:

$\displaystyle \left \{ {{25=V_C-V_T} \atop {30=V_C+V_T}} \right.$

Сложим уравнения и найдем Vc.:

$\displaystyle 55=2V_C\\V_C=27,5$

Собственная скорость лодки Vс.=27,5 км/ч

Найдем скорость течения реки:

$\displaystyle 25=27,5-V_T\\V_T=2,5$ (км/ч)

Найдем, на сколько км/ч скорость течения реки меньше собственной скорости лодки:

27,5 - 2,5 = 25 (км/ч)

0,0(0 оценок)

Ответ:

natashashvachka

07.04.2023 00:03

Покажем, что (cos x)'=-sin x

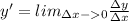
По определению $y'=lim_{\Delta x-0} \frac {\Delta y}{\Delta x}$

Приращение функции равно

$\Delta y=cos (x+\Delta x)-cos x=-2sin(x+\frac{\Delta x}{2})sin (\frac {\Delta x}{2})$

Ищем отношение

$\frac {\Delta y}{\Delta x}=-sin(x+\frac{\Delta x}{2})\frac {sin (\frac {\Delta x}{2})}{\Delta \frac{x}{2}}$

Перейдем в этом равенстве к границе, когда $\Delta x-0$ . В следствии непрерывности функции sin x

$lim_{\Delta x-0} -sin(x+\frac{\Delta x}{2})=- -sin lim_{\Delta x-0}(x+\frac{\Delta x}{2})=-sin x$

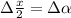Для второго множителя (используя один из замечательных пределов), обозначив $\Delta \frac {x}{2} =\Delta \alpha$ , имеем

$lim_{\Delta x-0} \frac {sin (\frac {\Delta x}{2})}{\Delta \frac{x}{2}}= lim_{\alpha-0} \frac {sin \alpha}{\alpha}=1$

Поєтому

$lim_{\Delta x-0} \frac {\Delta y}{\Delta x}=lim_{\Delta x-0} (-sin(x+\frac{\Delta x}{2})\frac {sin (\frac {\Delta x}{2})}{\Delta \frac{x}{2}})=-sin x *1=-sin x$

Т.е. (сos x)'=-sinx

Производная тангенса. Возьмем любую точку х є (a;b), где (a;b) - один из интервалов, на котором определена функция tg x. Ищем приращение

$\Delta y=\frac {sin (x+\Delta x)}{cos(x+\Delta x)}-\frac {sin x}{cos x}= =\frac{sin(x+\Delta x)cos x-sinx cos(x+\Delta x)}{cos(x+\Delta x)cos x}= \frac{sin \Delta x}{cos(x+\Delta x)cos x}$

Получаем отношение

$\frac {\Delta y}{\Delta x}=\frac{\frac {sin \Delta x}{\Delta x}}{cos(x+\Delta x)cos x}$

переходим к границе, когда $\Delta x-0$ .

$lim_{\Delta x-0}\frac {\Delta y}{\Delta x}=lim_{\Delta x-0}\frac{\frac {sin \Delta x}{\Delta x}}{cos(x+\Delta x)cos x}=\frac {1}{cos^2 x}$

Следовательно производная функции y=tg x существует и равна

$(tg x)'=\frac {1}{cos^2 x}$

0,0(0 оценок)

Популярные вопросы: Алгебра

иляяя1яяя

01.03.2020 17:25

Тема формула корней квадратного уравнения 1. -0,5x^2-7x-5=0 2. 2/3x^2+3/5x-3/4=0 знаю, что это не сложно, но когда в уравнении идёт вычисление 2-х корней, я всегда путаюсь...

alyvolkonskaya394638

01.04.2021 10:22

Найдите производную функции: [tex]y = arc \cos \frac{2x - 1}{ \sqrt{3} } [/tex]...

Dashboard18228

29.09.2022 04:38

Решить. на примере системы уравнений расскажите, как решают систему методом сложения. ...

Dhe32

30.09.2021 00:32

6x^2+5x+1 разложите квадратный трёхчлен на множители. сократите дробь: x^2-9/x^2-2x-15...

Tanya31323

05.05.2022 00:28

При якому значенні a пара чисел(1; -3) є розв язком рівняння. 1)2х-7у=а,2)6х-ау=4?...

elenalev222016

10.04.2020 10:06

8класс. решительно (х+3)⁴+(х+1)⁴=16...

koi4

04.09.2022 16:41

Tg a * корень из (1-ctg^2a)=корень из (ctg ^2 a - 1) это верно? если да,то объясните почему...

veronichkasape

08.07.2020 01:13

(2,3)в квадрате -0,6*2,3+(0,3)в квадрате ....

Масянька189

08.07.2020 01:13

13*x+17-(18*x+14)+(5*x-2) определите знак выражения надо...

sonikzets

04.03.2020 09:16

Найдите множество значений выражения: (-1) в степени n × (-1) в степени n+1 × (-1) в степени 2n+2 - 1° , при n = n...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку

Вычислите (cos (5x + 1)) ' Выберите один ответ: 1. 5sin x 2. 5cos (x + 1) 3. – 5sin (5x + 1)

Вычислите (cos (5x + 1)) ' Выберите один ответ:
1. 5sin x
2. 5cos (x + 1)
3. – 5sin (5x + 1)