Выберите равновозможные элементарные события.
Укажите один или несколько правильных вариантов ответа:
При одном бросании правильной игральной кости "выпало 2 очка" и "выпало 5 очков".
При одном бросании правильно игральной кости "выпало 2 очка" и "выпало 7 очков".
Подъехав к перекрёстку "автомобиль свернёт направо" и "автомобиль развернётся и поедет обратно"
При бросании правильной монеты "выпал орёл" и "выпала решка".

Показать ответ

Ответ:

Nathoe789

06.11.2021 11:51

Для того, чтобы решить уравнение х^4 - 5x^2 + 4 = 0, произведем замену:

t = x^2, получим квадратное уравнение:

t^2 - 5t + 4 = 0;

Ищем дискриминант:

D = b^2 - 4ac = (- 5)^2 - 4 * 1 * 4 = 25 - 16 = 9;

t1 = (-b + √D) / 2a = ( 5 + √9) / 2 * 1 = (5 + 3)/2 = 8/2 = 4;

t2 = (-b - √D) / 2a = ( 5 - √9) / 2 * 1 = (5 - 3)/2 = 2/2 = 1;

Возвращаемся к нашей замене и получаем два уравнения, которые нужно решить:

х^2 = 4 и x^2 = 1.

Из первого и второго уравнения получаем по два корня х1 = 2 и х2 = -2, а из второго х3 = 1 и х4 = -1.

ответ: х1 = 2; х2 = -2; х3 = 1; х4 = -1.

0,0(0 оценок)

Ответ:

sanya1897p08pyj

14.03.2020 09:33

$\frac{1 + \sqrt{x} + x}{1 + \sqrt{x} } = \frac{1 + \sqrt{x} + x }{1 + \sqrt{x} } \times \frac{1 - \sqrt{x} }{1 - \sqrt{x} } = \frac{(1 + \sqrt{x} + x)(1 - \sqrt{x}) }{(1 + \sqrt{x} )(1 - \sqrt{x}) } = \frac{ {1}^{3} - {( \sqrt{x} )}^{3} }{1 - x} = \frac{1 - x \sqrt{x} }{1 - x}$

Пояснение:

Выражения такого типа, когда в знаменателе сумма или разность числа и числа под корнем, избавляются от иррациональности простым методом. Вспоминаем формулу сокращенного умножения, разность квадратов:

${a}^{2} - {b}^{2} = (a - b)(a + b)$ . В нашем примере в знаменателе сумма, то есть (a + b) из формулы. Нам нужно найти (a - b) и умножить на это дробь, чтобы потом получилось ${a}^{2} - {b}^{2}$ , а ${( \sqrt{x} )}^{2} = x$ , получится просто число, таким образом избавимся от корня в знаменателе. В нашем случае — это , — это $\sqrt{x}$ . Соответственно, (a - b) — это $(1 - \sqrt{x} )$ .

Важно отметить, что нужно умножить наше выражение не просто на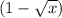 $(1 - \sqrt{x} )$ , а на 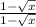$\frac{1 - \sqrt{x} }{1 - \sqrt{x} }$ , потому что 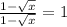$\frac{1 - \sqrt{x} }{1 - \sqrt{x} } = 1$ , а при умножении на 1 значение выражения не измениться. Если умножить просто на 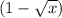$(1 - \sqrt{x} )$ значение выражения поменяется.