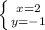Количество ступенек, насчитанных мальчиком при подъеме, в 5 раз больше, чем при спуске т.к.
225/45=15²/(15*3)=15/3=5. когда он бежит вверх, ему показывается ступенек в пять раз больше, чем когда он опускается.
Если он сбежит пять раз вниз, то насчитает 225 ступенек, а уйдут от него ступенек столько же, сколько их было при движении вверх, получается, что 225+225=450- это количество ступенек, просчитанных шесть раз. тогда 450/6=75- столько ступенек он насчитал бы, пройдя по неподвижному эскалатору.
Есть несколько методов решения систем уравнений с двумя неизвестными, например,
1) метод сложения - уравнения складываются, чтобы получить уравнение с одной переменной
2) метод подстановки - одна переменная выражается через другую из одного уравнения и подставляется во второе уравнение
3) метод почленного умножения(деления) - одно уравнение делится на другое
Первую систему можно решить методом сложения или подстановки
Сложение
Если сложить уравнения, получится новое уравнение. в котором только переменная x:
x^2 + 2 = x + 8
x^2 - x + 6 = 0
x^2 - 3x + 2x - 6 = 0
x(x - 3) + 2(x - 3) = 0
(x - 3)(x + 2) = 0
x = 3 или x = -2
y можно найти из первого уравнения системы:
x = 2 + y
x= 3 x = -2
3 = 2 + y -2 = 2 + y
y = 1 y = -4
ответ: ;
Подстановка
В первом уравнении x уже выражено через y
x = y + 2
Подставим y + 2 вместо x во второе уравнение:
(y + 2)^2 - y = 8
y^2 + 4y + 4 - y = 8
y^2 + 3y - 4 = 0
y^2 + 4y - y -4 = 0
y(y + 4) - 1(y + 4) = 0
(y - 1)(y + 4) = 0
y = 1 или y = -4
x находим из первого уравнения:
x = y + 2
y = 1 y = -4
x = 1 + 2 = 3 x = -4 + 2 = -2
Вторую систему можно также решать методом подстановки или сложения, более удобным будет, вероятно, метод сложения(для первой системы был удобнее метод подстановки)
Решение методом сложения:
Второе уравнение домножим на -1:
-x - y = -1
и сложим с первым:
3x + y - x - y = 1 - 1
2x = 0
x = 0
Из второго уравнения находим y;
x + y = 1
0 + y = 1
y = 1
ответ:
P. S. можно попробовать решить методом подстановки, но это будет дольше
Третья система решается методом почленного умножения(деления)
Первое уравнение раскладывается на множители:
x^2 - y^2 = (x + y)(x - y) = 3
Теперь первое уравнение модно разделить на второе (x + y 0):
=
Получается уравнение
x - y = 3 ( * )
Заменим первое уравнение системы на полученное уравнение ( * ), получим эквивалентную систему, которую можно решить методом сложения:
Количество ступенек, насчитанных мальчиком при подъеме, в 5 раз больше, чем при спуске т.к.
225/45=15²/(15*3)=15/3=5. когда он бежит вверх, ему показывается ступенек в пять раз больше, чем когда он опускается.
Если он сбежит пять раз вниз, то насчитает 225 ступенек, а уйдут от него ступенек столько же, сколько их было при движении вверх, получается, что 225+225=450- это количество ступенек, просчитанных шесть раз. тогда 450/6=75- столько ступенек он насчитал бы, пройдя по неподвижному эскалатору.
Объяснение:
Есть несколько методов решения систем уравнений с двумя неизвестными, например,
1) метод сложения - уравнения складываются, чтобы получить уравнение с одной переменной
2) метод подстановки - одна переменная выражается через другую из одного уравнения и подставляется во второе уравнение
3) метод почленного умножения(деления) - одно уравнение делится на другое
Первую систему можно решить методом сложения или подстановки
Сложение
Если сложить уравнения, получится новое уравнение. в котором только переменная x:
x^2 + 2 = x + 8
x^2 - x + 6 = 0
x^2 - 3x + 2x - 6 = 0
x(x - 3) + 2(x - 3) = 0
(x - 3)(x + 2) = 0
x = 3 или x = -2
y можно найти из первого уравнения системы:
x = 2 + y
x= 3 x = -2
3 = 2 + y -2 = 2 + y
y = 1 y = -4
ответ: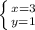 ;
; 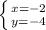
Подстановка
В первом уравнении x уже выражено через y
x = y + 2
Подставим y + 2 вместо x во второе уравнение:
(y + 2)^2 - y = 8
y^2 + 4y + 4 - y = 8
y^2 + 3y - 4 = 0
y^2 + 4y - y -4 = 0
y(y + 4) - 1(y + 4) = 0
(y - 1)(y + 4) = 0
y = 1 или y = -4
x находим из первого уравнения:
x = y + 2
y = 1 y = -4
x = 1 + 2 = 3 x = -4 + 2 = -2
Вторую систему можно также решать методом подстановки или сложения, более удобным будет, вероятно, метод сложения(для первой системы был удобнее метод подстановки)
Решение методом сложения:
Второе уравнение домножим на -1:
-x - y = -1
и сложим с первым:
3x + y - x - y = 1 - 1
2x = 0
x = 0
Из второго уравнения находим y;
x + y = 1
0 + y = 1
y = 1
ответ: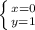
P. S. можно попробовать решить методом подстановки, но это будет дольше
Третья система решается методом почленного умножения(деления)
Первое уравнение раскладывается на множители:
x^2 - y^2 = (x + y)(x - y) = 3
Теперь первое уравнение модно разделить на второе (x + y 0):
0):
Получается уравнение
x - y = 3 ( * )
Заменим первое уравнение системы на полученное уравнение ( * ), получим эквивалентную систему, которую можно решить методом сложения:
x - y + x + y = 4
2x = 4
x = 2
x - y = 3
2 - y = 3
y = -1
ответ: