По формуле n-го члена геометрической прогрессии: :
Решая как квадратное уравнение, получим
Тогда:
Так как b1 * b2 = (-27/4) * 9 < 0, то отбрасываем. И так как 27*9 > 0, то удовлетворяет условию только b1 = 27 и знаменатель прогрессии q=1/3.
третий член:
ответ: b1 = 27; b3 = 3.
По формуле n-го члена геометрической прогрессии: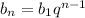 :
:
Решая как квадратное уравнение, получим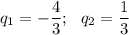
Тогда: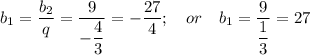
Так как b1 * b2 = (-27/4) * 9 < 0, то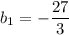 отбрасываем. И так как 27*9 > 0, то удовлетворяет условию только b1 = 27 и знаменатель прогрессии q=1/3.
отбрасываем. И так как 27*9 > 0, то удовлетворяет условию только b1 = 27 и знаменатель прогрессии q=1/3.
третий член: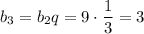
ответ: b1 = 27; b3 = 3.