Во время большой перемены две восьмиклассницы играют в теннис на прямоугольном корте, длина которого вдвое больше ширины, а площадь равна 800 м2 Найдите размеры корта и расстояние между девушками, если они встанут по диагонали прямоугольной площадки

2)
1,3^(5x-1) -1,3^(5x-3) > 0 ,69 ⇔ 1,3^(5x-3) *(1,3² -1) >  0 ,69 ⇔
1,3^(5x-3) *(1,69 -1) >  0 ,69 ⇔1,3^(5x-3) *0,69 > 0 ,69 ⇔1,3^(5x-3) > 1⇔
1,3^(5x-3)  > 1,3⁰ ⇔ 5x-3 >0  ⇔x > 3 / 5 .     || т.к. 1,3 >1 || 
наименьшее целое решение неравенств  будет 1.

ответ : 1.

3.
0,6 ^ x > 3 ^x ;⇔ (3/0,6) ^x  < 1 ⇔5^x < 5⁰⇒ x <0
наибольшее целое решение неравенства  будет  -1 .

ответ :  -1.

4.
0,5^x  ≤ 4^x  ⇔  1 ≤ (4 /0,5) ^x ⇔8^x  ≥8 ⁰⇒ x  ≥ 0.

ответ : x∈ [ 0 ; ∞).

5.
7,1^ ((x²+3) /(x-5) ) ≥1⇔ 7,1^ ((x²+3) /(x-5) ) ≥7,1⁰ ⇔ (x²+3) /(x-5 ) ≥ 0 ⇒
x >0 .

ответ : x∈ ( 0 ; ∞).

a) Вероятность взять один синий карандаш, равна 5/9. В коробке останется 8 карандашей. Вероятность взять второй синий карандаш, равна 4/8 = 1/2, вероятность взять третий сини карандаш равна 3/7. По теореме умножения, 5/9 * 1/2 * 3/7 = 5/42

Аналогично вероятность взять один красный карандаш равна 4/9, второй красный карандаш - 3/8, третий красный карандаш - 2/7. По теореме умножения, 4/9 * 3/8 * 2/7 = 1/21

По теореме сложения, вероятность взять 3 карандаша одинакового цвета равна 5/42 + 1/21 = 5/42 + 2/42 = 7/42 = 1/6

б) Всего всевозможных исходов: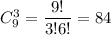 из них нужно взять 2 синих и 1 красный карандаш, таких у нас 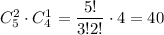. Вероятность того, что среди отобранных 3 карандаша 2 синих и 1 красный карандаш, равна 40/84 = 10/21

c) Вероятность того, что среди наугад выбранных 3 карандаша нет синего цвета, равна 1/21 (посчитали в пункте а), тогда вероятность того, что среди них будет хотя бы 1 карандаш синий, равна 1 - 1/21 = 20/21