Вертикаль бүрыштардың бисектрисалары бір түзудің бойында жататынын дәллелдеңдер​

х--длина ровного участка
у--длина подъема из А в В.      если ехать из В в А,у будет длина спуска,а 0,7у длина 
0,7у--длина спуска из А в В      подъема. т.е. наоборот
24мин=2/5часа.
сост.уравн.
(х/25+у/15+0,7у/30)-(х/25+у/30+ 0,7у/15)=2/5.
у/15+0,7у-у/30-0,у/15=2/5
0,3у=12
у=40--т.е. длина подъема равна 40км.из А в В
40*0,7=28---длина спуска из А в В 
40+28=68; 78-68=10км--ДЛИНА РОВНОГО УЧАСТКА ДОРОГИ.
10/25+28/15+40/30=3,18/30 или 3ч 36 мин. но мы не знаем где было больше подъемов из А в В или из В в А,поэтому делаем проверку
10/25+28/30+40/15=120/30=4часа. т.к. 
значит 3ч,36мин
ответ:10км;3ч,36мин 

Перепишем уравнение, учитывая, что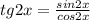

-----(1)

В уравнение (1) выражение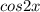 находится в знаменателе, поэтому 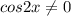, или 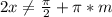 , 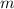- целое

или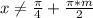  , 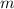- целое-----(2)

Сократим в левой части уравнения (1) на :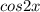

  , отсюда , отсюда

  , или ,  - целое ------(3)

Из решений (3) надо исключить значения, равные значениям (2):

 , отсюда

  , сокращая на , получим

  - нечетные числа 

Другими словами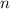 принимает только четные значения!

 Из условия следует, что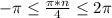 , отсюда

Таким образом,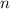 принимает значения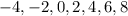 

Видно, что решения (3) уравнения составляют арифметическую прогрессию с первым членом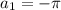 и последним седьмым членом

Теперь мы можем найти сумму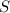  всех решений уравнения как сумму первых семи членов арифметической прогрессии: