В задаче 1 нужно дать ответ и коротко его обосновать.
1) Определите истинность данных утверждений.
a) Если расстояние между центрами двух окружностей больше суммы их диаметров, то эти
окружности не имеют общих точек.
b) Катет прямоугольного треугольника, прилежащий к углу 30°, равен половине
гипотенузы.
c) Один из углов треугольника всегда не превышает 60 градусов.
d) Любой равнобедренный треугольник можно разрезать на два равных прямоугольных
треугольника.
e) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы
составляют в сумме 90°, то эти две прямые параллельны.
f) Если две прямые параллельны третьей, то они параллельны друг другу.
g) Биссектрисы смежных углов перпендикулярны.
h) Расстоянием от точки до прямой называется длина отрезка, соединяющего данную точку
с произвольной точкой данной прямой.
i) Медиана равностороннего треугольника делит его угол на два равных.
В задачах 2 – 5 нужно записать полное решение, включающее «Дано» и чертѐж.
2) Две стороны тупоугольного равнобедренного треугольника равны 6 см и 1 дм. Найдите
периметр этого треугольника.
3) Внешний угол треугольника ABC при вершине A равен 52°. Через вершину B проведена
прямая DE так, что угол ABD =128 , а BC – биссектриса угла ABE. Докажите, что AC = AB.
4) В равнобедренном треугольнике угол при основании в 4 раза меньше угла,
противолежащего основанию, а боковая сторона равна 13 дм. Найдите медиану,
проведѐнную к основанию этого треугольника.
5) В треугольнике ABC угол C прямой. Точка M лежит на стороне AC. Докажите,
что BC < BM < AB.
В задаче 6 нужно выполнить построение с циркуля и линейки, описать
последовательность действий при построении и проанализировать количество решений,
которые имеет данная задача.
6) Постройте угол, равный 30°.
Парабола и прямая пересекаются в двух точках: (-20;80) и (5;5).
Объяснение:
Парабола y = 1/5x2 и прямая y = 20 - 3x пересекаются, если эта система имеет решение.
y = 1/5x2,
y = 20 - 3x;
1/5x2 = 20 - 3x;
1/5x2 + 3x - 20 = 0 (умножим на 5);
5x2 + 15x - 100 = 0;
Легко найти корни по теореме, обратной теореме Виета (можно и по формуле корней).
x1 = -20, x2 = 5.
Тогда y1 = 20 - 3 * (-20) = 20 + 60 = 80,
y2 = 20 - 3 * 5 = 20 - 15 = 5.
Парабола и прямая пересекаются в двух точках: (-20;80) и (5;5).
x = 7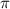
/6
Объяснение:
2 sin x = -1
sin x = -0.5
Отмечаем нужные точки на тригонометрическом круге
Это x = -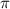
/6 + 2
Так же можно задать это множество решений так:
x =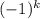
* (-
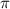/6) +
Нам нужно выбрать из множества решений только те, которые принадлежат заданному промежутку.
Отметим этот промежуток на тригонометрическом круге
Из рисунка видно, что подходит только одно решение x = 7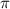
/6
Это решение можно было найти другим решив неравенство
1/2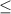
7/6 + 2k
3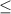
7 + 12k
Так как k - целое, то подходит только k = 0, при других целых k неравенство не выполняется.
1/2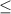
-1/6 + 2k
3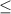
-1 + 12k
Здесь нет целых значений k, для которых бы выполнялось неравенство (при k = 0 -1+0<3, при k = 1 -1+11>9)
Значит, решением является только x = 7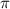
/6
Но здесь проще находить решение именно из тригонометрического круга по рисунку.