В турнире по шахматам принимают участие мальчики и девочки. За победу в шахматной партии начисляют 1 очко, за ничью — 0,5 очка, за проигрыш — 0 очков. По правилам турнира каждый участник играет с каждым другим дважды. Сколько девочек могло принимать участие в турнире, если известно, что их в 9 раз меньше, чем мальчиков, и что мальчики набрали в сумме ровно в четыре раза больше очков, чем девочки? уровень 8 класса

Будем искать ответ в виде у=a*sin(b*x+c)+d

максимум функции равен а+d=4 (по графику)

минимум функции равен –a+d=-2 (по графику)

сложим оба уравнения и получим 2d=4-2=2 отсюда d=1

вычтем оба уравнения и получим 2a=4+2=6 отсюда a=3

далее ищем ответ в виде у=3*sin(w*x+c)+1

w=2pi/T где T – период

по графику видно что расстояние между двумя максимумами равно 4pi

значит T=4pi

w=2pi/4pi=1/2

далее ищем ответ в виде у=3*sin(x/2+c)+1

при х=0 имеем  

у(х=0)=3*sin(0/2+c)+1=3*sin(c)+1=2,5 (по графику)

3*sin(c)+1=2,5

sin(c) = 0,5

c1=pi/6+2pi*k

c2=pi-pi/6+2pi*k=5pi/6+2pi*k

по графику при х ~ 0 график возрастает

3*sin(x/2+c)+1 ~ 3*sin(c)+1

sin(t) при t ~ pi/6 – возрастает

sin(t) при t ~ 5pi/6 – убывает – значит с2 не подходят нам

далее ищем ответ в виде у=3*sin(x/2+c)+1 где с = pi/6+2pi*k

диапазону от 0 до 2pi принадлежит с = pi/6

ответ 1) у=3*sin(x/2+pi/6)+1  

далее ищем ответ в виде у=3*sin(x/2+c)+1 где с = pi/6+2pi*k

диапазону от -2pi до 0 принадлежит с = pi/6-2pi = -11pi/6

ответ 2) у=3*sin(x/2-11pi/6)+1

воспользуемся формулами приведения

sin(t)=sin(pi-t)

применим к ответу 1)

у=3*sin(x/2+pi/6)+1= 3*sin(pi-(x/2+pi/6))+1= 3*sin(-x/2+5pi/6)+1

ответ 3) у= 3*sin(-x/2+5pi/6)+1

от аргумента отнимем 2pi

у= 3*sin(-x/2+5pi/6)+1 = 3*sin(-x/2+5pi/6-2pi)+1= 3*sin(-x/2-7pi/6)+1

ответ 4) у= 3*sin(-x/2-7pi/6)+1

теперь надо перейти к косинусу

желательно чтобы знаки аргумента и функции не менялись

перейти к косинусу можно при формул приведения

sin(t)=cos(pi/2-t) (a)

sin(t)=-cos(pi/2+t) (b)

sin(t)=-cos(3pi/2-t) (c)

sin(t)=cos(3pi/2+t) (d)

применю (d) к формуле ответа 1)

у=3*sin(x/2+pi/6)+1= 3*cos(x/2+pi/6+3pi/2)+1= 3*cos(x/2+10pi/6)+1

ответ 5) у=3*cos(x/2+5pi/3)+1

отнимем от аргумента 2pi

у=3*cos(x/2+5pi/3)+1=3*cos(x/2+5pi/3-2pi)+1=3*cos(x/2-pi/3)+1

ответ 6) у=3*cos(x/2-pi/3)+1

так как cos(t)=cos(-t)

ответ 7) у=3*cos(-x/2+pi/3)+1

отнимем от аргумента 2pi

ответ 8) у=3*cos(-x/2-5pi/3)+1

1.

ОДЗ: арксинус определен при

Найдем синус левой и правой части:

Уравнение распадается на два. Для первого уравнения получим:

Решаем второе уравнение:

Таким образом, уравнение имеет единственный корень 0.

ответ: 0

2.

ОДЗ: арксинус определен при

Найдем синус левой и правой части:

Так как в правой части стоит положительная величина, то и левая часть должна быть положительной, то есть .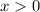

Возведем в квадрат обе части:

Решим биквадратное уравнение:

Находим х:

Однако, так как было выявлено ограничение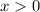 , то отрицательный корень не попадает в ответ.

Оценив значение полученного корня, мы понимаем, что он удовлетворяет исходной ОДЗ:

ответ: