Возможны две ситуации взаимного расположения этих точек: и .
Заметим, что первая ситуация не дает решений, так как при выражение в правой части уравнения , но с другой стороны это выражение есть сумма модулей, которая не может быть отрицательной. Значит, при уравнение не имеет решений.
Рассмотрим ситуацию . Раскроем модуль при трех условиях:
1. Пусть . Тогда оба модуля раскрываются со сменой знака:
Но по условию раскрытия модулей . Значит, в данном случае корней нет.
2. Пусть . Тогда первый модуль раскрывается без смены знака, а второй - со сменой знака:
Это верное равенство. Значит, решениями являются все значения, при которых было сделано такое раскрытие модулей:
3. Пусть . Тогда оба модуля раскрываются без смены знака:
Но по условию раскрытия модулей . Значит, в данном случае корней нет.
Таким образом, корни имеются только при условии . Они определяются соотношением .
Выделив условие как частный случай, можно записать ответ.
Найдем нули подмодульных выражений:
Возможны две ситуации взаимного расположения этих точек: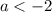
и 
.
Заметим, что первая ситуация не дает решений, так как при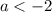
выражение в правой части уравнения 
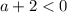, но с другой стороны это выражение есть сумма модулей, которая не может быть отрицательной. Значит, при 
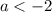уравнение не имеет решений.
Рассмотрим ситуацию
. Раскроем модуль при трех условиях:
1. Пусть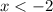
. Тогда оба модуля раскрываются со сменой знака:
Но по условию раскрытия модулей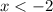
. Значит, в данном случае корней нет.
2. Пусть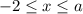
. Тогда первый модуль раскрывается без смены знака, а второй - со сменой знака:
Это верное равенство. Значит, решениями являются все значения, при которых было сделано такое раскрытие модулей:
3. Пусть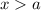
. Тогда оба модуля раскрываются без смены знака:
Но по условию раскрытия модулей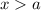
. Значит, в данном случае корней нет.
Таким образом, корни имеются только при условии
. Они определяются соотношением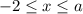 
.
Выделив условие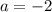
как частный случай, можно записать ответ.
при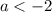
: нет корней
при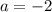
: один корень 
при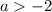
: бесконечное множество корней: ![x\in[-2;\ a]](/tpl/images/1359/9802/14c1d.png)
№183.
18 (км/час) - скорость лодки по течению.
15 (км/час) - скорость лодки против течения.
№184.
85 яблок во втором ящике.
175 яблок в первом ящике.
Объяснение:
№183.
Формула движения: S=v*t
S - расстояние v - скорость t – время
х - собственная скорость лодки.
у - скорость течения реки.
х+у - скорость лодки по течению.
х-у - скорость лодки против течения.
Согласно условию задачи составляем систему уравнений:
(х+у)*3+(х-у)*4=114
(х-у)*6=(х+у)*5
Раскрыть скобки:
3х+3у+4х-4у=114
6х-6у=5х+5у
Привести подобные члены:
7х-у=114
х=11у
Подставить выражение х через у из второго уравнения в первое и вычислить у:
7*11у-у=114
77у-у=114
76у=114
у=114/76
у=1,5 (км/час) - скорость течения реки.
х=11*1,5
х=16,5 (км/час) - собственная скорость лодки.
16,5+1,5=18 (км/час) - скорость лодки по течению.
16,5-1,5=15 (км/час) - скорость лодки против течения.
Проверка:
15*6=18*5
90=90
№184.
х - яблок в первом ящике.
у - яблок во втором ящике.
Согласно условию задачи составляем систему уравнений:
х-45=у+45
3(у-20)=х+20
Раскрыть скобки:
х-45=у+45
3у-60=х+20
Привести подобные члены:
х=у+90
3у=х+80
Подставить выражение х через у из первого уравнения во второе и вычислить у:
3у=у+90+80
2у=170
у=85 - яблок во втором ящике.
х=85+90
х=175 - яблок в первом ящике.
Проверка:
175-45=130
85+45=130
130=130.