В двух автобусах ехали 46 пассажиров. На остановке из первого вышли 7 пассажиров, из второго вышли 13 пассажиров, а вошли – в первый 28 пассажиров, в второй 20 пассажиров. После остановки в автобусах людей стало поровну. Сколько пассажиров было в каждом автобусе до остановки?

Показать ответ

Ответ:

Danulchukik

21.01.2021 01:35

№1

а) √50 > 7

√50 > √7²

√50 > √49

б) 4√6 > 3√7

√4²*6 > √3²*7

√16*6 > √9*7

√96 > √63

№2

а) √(196 * 0,64) = √(14²*(0,8)²) = 14 * 0,8 = 11,2

б) √(72*0,5)=√36=√6² = 6

в)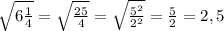 $\sqrt {6\frac{1}{4}} = \sqrt{\frac{25}{4} } =\sqrt{\frac{5^{2} }{2^{2} } }=\frac{5}{2} =2,5$

г) √(-2)⁶ = √((-2)³)²=(-2)³= - 8

№3

а) (√3+√2)² = (√3)²+ 2 *√3*√2 + (√2)²= 3 + 2√6 + 2 = 5 +2√6

б) (4 - √5)(4 + √5) = 4² - (√5)² = 16 - 5 = 11

в) 5√12 - 2√27 - 3√3 = 5√(4*3) - 2√(9*3) - 3√3 = 5√(2²*3) - 2√(3²*3) - 3√3 = 5*2√3 - 2*3√3 - 3√3= 10√3 - 6√3 - 3√3 = √3

№4

√(72*а⁵) = √(36*2 * а⁴*а)= √(6²*2 * (а²)² * а) = 6*а²*√(2а)

№5

$\frac{x+y\sqrt{2} }{x^{2} - 2y^{2} } = \frac{x+y\sqrt{2} }{(x+y\sqrt{2} )(x-y\sqrt{2}) } = \frac{1}{(x-y\sqrt{2})}$

№6

$a) \frac{5}{\sqrt{13} } =\frac{5*\sqrt{13} }{\sqrt{13}*\sqrt{13} }=\frac{5*\sqrt{13}}{13 } \\b) \frac{1}{\sqrt{13} -2 } = \frac{1*(\sqrt{13} +2)}{(\sqrt{13} -2)(\sqrt{13} +2) }= \frac{\sqrt{13} +2}{13-4 }= \frac{\sqrt{13} +2}{9 }$

0,0(0 оценок)

Ответ:

ighjkhh

10.03.2022 07:07

1) не является; 2) не является

Объяснение:

1) Является ли у функцией х, если у - это число десятых в десятичной записи числа х?

У некоторых чисел существует 2 формы десятичной записи: с 0 и с 9 в периоде.

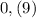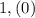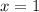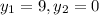Например, для числа 1 существуют 2 формы: 0,(9) и 1,(0) . В первом случае число десятых равно девяти, а во втором - нулю. То есть существует значение переменной x=1 , которому соответствуют несколько значений y_1=9,y_2=0 .

Значит, у не является функцией х.

2) Является ли x функцией y, если у - это число десятых в десятичной записи числа х?

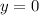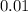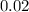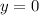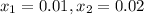Рассмотрим y=0 . Но число десятых у чисел 0.01 и 0.02 равно нулю. То есть существует значение переменной y=0 , которому соответствуют несколько значений (например, x_1=0.01,x_2=0.02 ).