Легко видеть,что х=1,у=1 -решение системы. Покажем, что других решений нет. Пусть х и у одного знака и не равны 0. Тогда понятно, что первое уравнение имеет 1 целочисленный корень (все слагаемые положительны).
Преобразуем первое уравнение: x^2+(x+0,5у)^2-0,25у^2+9y^2=12 x^2+(x+0,5у)^2+8,75y^2=12
Очевидно, что если х или у равен 1,или -1, то значение другой переменной не может быть по модулю больше 1. Первому уравнению удовлетворяет пара х=-1,у=-1, но она не удовлетворяет второму уравнению. Остается проверить х=0 или у=0 и убедиться, что таких решений нет.
Заметим, что дает такой же остаток при делении на s, что и . (Доказывается, например, так. Раскрываем скобки:
Очевидно, на каждом шаге будет образовываться слагаемое, делящееся на qs, и степень умноженная на r. Все слагаемые первого типа на остаток не влияют, так что остается только )
Кроме того, остаток от деления от суммы равен остатку от деления от суммы остатков (as + b + cs + d = (a + c)s + (b + d) дает такой же остаток при делении на s, что и b + d), а так же произведение можно менять на произведение остатков
Покажем, что других решений нет.
Пусть х и у одного знака и не равны 0. Тогда понятно, что первое уравнение имеет 1 целочисленный корень (все слагаемые положительны).
Преобразуем первое уравнение:
x^2+(x+0,5у)^2-0,25у^2+9y^2=12
x^2+(x+0,5у)^2+8,75y^2=12
Очевидно, что если х или у равен 1,или -1, то значение другой переменной не может быть по модулю больше 1. Первому уравнению удовлетворяет пара х=-1,у=-1, но она не удовлетворяет второму уравнению.
Остается проверить х=0 или у=0 и убедиться, что таких решений нет.
Заметим, что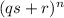
дает такой же остаток при делении на s, что и 
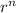. (Доказывается, например, так. Раскрываем скобки:
Очевидно, на каждом шаге будет образовываться слагаемое, делящееся на qs, и степень умноженная на r. Все слагаемые первого типа на остаток не влияют, так что остается только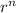
)
Кроме того, остаток от деления от суммы равен остатку от деления от суммы остатков (as + b + cs + d = (a + c)s + (b + d) дает такой же остаток при делении на s, что и b + d), а так же произведение можно менять на произведение остатков
Применяем наблюдения: