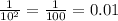мы можем записать это дробью, чтобы было легче вычислять.
при одинаковых основаниях (одинаковых больших буквах или цифрах) мы можем сложить степени, если мы перемножаем числа. также можем вычитать их, если числа делим, то бишь 14+9=23. получилось . теперь мы имеем такую дробь: . дробную черту можно заменить делением, а значит степени можно вычесть. не пугайтесь, что мы вычитаем из большего меньшее. теперь мы имеем следующее: . минусовую степень мы переворачиваем, получаем обыкновенную дробь. в числитель ставим единицу, а вниз - число в степени: . дальше всё просто: подставляем число и решаем.
В решении.
Объяснение:
1) x²-10x+25 ≤ 0
x²-10x+25 = 0
D=b²-4ac =100-100=0 √D=0
х₁,₂=(-b±√D)/2a
х₁,₂=(10±0)/2 = 5;
Уравнение квадратичной функции, график - парабола, ветви направлены вверх, парабола стоит на оси Ох.
Решение неравенства x={5}. ответ c).
2) -x²+x-210 ≤ 0
-x²+x-210 = 0/-1
x²-x+210 = 0
D=b²-4ac =1 - 840 = -839
D < 0
Уравнение не имеет действительных корней.
Значит, неравенство выполняется всегда или не выполняется никогда.
Подставить в неравенство произвольное значение х:
х = 0;
-0 + 0 -210 < 0, выполняется.
Значит, неравенство верно при любом значении х.
Решение неравенства: х∈(-∞; +∞). Вся числовая прямая. ответ b).
3) -x²-8x-15 ≤ 0
-x²-8x-15 = 0/-1
x²+8x+15 = 0
D=b²-4ac =64 - 60 = 4 √D=2
х₁=(-b-√D)/2a
х₁=(-8-2)/2 = -5;
х₂=(-b+√D)/2a
х₂=(-8+2)/2 = -3.
Уравнение квадратичной функции, график - парабола, ветви направлены вниз, парабола пересекает ось Ох в точках х = -4 и х= -3.
Решение неравенства х∈(-∞; -5]∪[-3; +∞). ответ f).
4) -x²+16<0
-x²+16=0
-x²= -16
x²= 16
х=±√16
х=±4.
Уравнение квадратичной функции, график - парабола, ветви направлены вниз, парабола пересекает ось Ох в точках х = -4 и х= 4.
Решение неравенства х∈(-∞; -4)∪(4; +∞). ответ f).
a) Неравенство не имеет решений
b) Решением неравенства является вся числовая прямая
c) Решением неравенства является одна точка.
d) Решением неравенства является закрытый промежуток.
e) Решением неравенства является открытый промежуток.
f) Решением неравенства является объединение двух промежутков.
мы можем записать это дробью, чтобы было легче вычислять.
при одинаковых основаниях (одинаковых больших буквах или цифрах) мы можем сложить степени, если мы перемножаем числа. также можем вычитать их, если числа делим, то бишь 14+9=23. получилось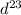 . теперь мы имеем такую дробь:
. теперь мы имеем такую дробь: 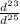 . дробную черту можно заменить делением, а значит степени можно вычесть. не пугайтесь, что мы вычитаем из большего меньшее. теперь мы имеем следующее:
. дробную черту можно заменить делением, а значит степени можно вычесть. не пугайтесь, что мы вычитаем из большего меньшее. теперь мы имеем следующее: 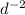 . минусовую степень мы переворачиваем, получаем обыкновенную дробь. в числитель ставим единицу, а вниз - число в степени:
. минусовую степень мы переворачиваем, получаем обыкновенную дробь. в числитель ставим единицу, а вниз - число в степени: 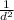 . дальше всё просто: подставляем число и решаем.
. дальше всё просто: подставляем число и решаем.