Поскольку под радикалами суммы квадратов, то ОДЗ для подкоренных выражений писать ненужно.
Сделаем замены:
Тогда :
Но тогда, нужно записать следующие ограничения:
Теперь можно возвести в квадрат и домножить на 2 первое уравнение системы:
То есть нужно изобразить множество точек :
Прямые и параллельны.
Найдем точки пересечения не параллельных прямых:
Таким образом, график это отрезок прямой с координатами концов: (-1;2) и (2;-1) (смотрите рисунок 1)
Теперь вторая часть задания.
Найти все значения параметра a, что кривая :
имеет с полученным выше отрезком ровно одну общую точку. Иначе говоря, уравнение имеет одно решение при условии:
График - это график смещенный на единицу вправо по оси x.
График - классическая парабола c ветвями вниз смещенная вверх на по оси .
Графически понятно, что одно решение будет либо когда парабола касается левой ветки модуля в одной точке (1) (синяя парабола), либо когда парабола находится между красной и зеленой параболой включительно, то есть параболами пересекающими края отрезка (2).
Смотрите рисунок 2.
1. Найдем эти пограничные a:
∈(3;5]
2. Определим a, в случае касания параболы левой ветки модуля, то есть когда уравнение :
1)
область определения (-∞;+∞)
множество значений (-∞;4,5]
точка пересечения с осью Оу (0; 2,5)
положительна на (-3;1)
отрицательна на (-∞;-3) и (1;+∞)
2)
область определения (-∞;+∞)
множество значений [-2;+∞)
точка пересечения с осью Оу (0; 1)
положительна на (-∞;1) и (5;+∞)
отрицательна на (1;5)
3)
область определения [3;7]
множество значений [-1;5]
точка пересечения с осью Оу (0; 4)
положительна на [-3;4] и (5;7]
отрицательна на (4;5)
4)
область определения (-∞;2)U(2;+∞)
множество значений (-∞;1)U(1;+∞)
точка пересечения с осью Оу (0; 1,5)
положительна на (-∞;2) и(3;+∞)
отрицательна на (2;3)
1) Отрезок прямой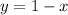 при
при 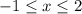 (cмотрите рисунок 1)
(cмотрите рисунок 1)
2) ∈{0,75} ∪ (3;5]
∈{0,75} ∪ (3;5]
Объяснение:
Поскольку под радикалами суммы квадратов, то ОДЗ для подкоренных выражений писать ненужно.
Сделаем замены:
Тогда :
Но тогда, нужно записать следующие ограничения:
Теперь можно возвести в квадрат и домножить на 2 первое уравнение системы:
То есть нужно изобразить множество точек :
Прямые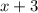 и
и 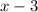 параллельны.
параллельны.
Найдем точки пересечения не параллельных прямых:
Таким образом, график это отрезок прямой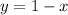 с координатами концов: (-1;2) и (2;-1) (смотрите рисунок 1)
с координатами концов: (-1;2) и (2;-1) (смотрите рисунок 1)
Теперь вторая часть задания.
Найти все значения параметра a, что кривая :
График - это график
- это график 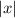 смещенный на единицу вправо по оси x.
смещенный на единицу вправо по оси x.
График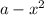 - классическая парабола
- классическая парабола 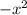 c ветвями вниз смещенная вверх на
c ветвями вниз смещенная вверх на  по оси
по оси 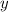 .
.
Графически понятно, что одно решение будет либо когда парабола касается левой ветки модуля в одной точке (1) (синяя парабола), либо когда парабола находится между красной и зеленой параболой включительно, то есть параболами пересекающими края отрезка (2).
Смотрите рисунок 2.
1. Найдем эти пограничные a:
2. Определим a, в случае касания параболы левой ветки модуля, то есть когда уравнение :
имеет единственное решение, то есть когда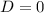
Таким образом, 1 решение при: