Укажите простое предложение, в котором должно стоять тире между подлежащим и сказуемым. Знаки препинания не расставлены. а) Алатырь волшебный камень упоминаемый в русских заговорах легендах и сказках.

б) Отважный пловец решил в такую ночь пуститься через пролив на расстояние двадцати вёрст.

в) Привлечённые светом бабочки прилетали и кружились около фонарей.

г) Духовную крепость нельзя взять штурмом и разрушить.

1)В этих задачах не меняется сухая часть, то есть мякоть, из которой состоит фрукт. Поэтому находим сухую часть в сухофруктах, чья доля равна 1-0,21=0.79

5×(1-0,21)=3,95 кг

Теперь находим ту самую мякоть в свежих сливах

1-0,84=0,16

И теперь находим необходимое количество слив для 5 кг сухофруктов

3,95÷0,16≈24,7 кг

ответ:24,7 кг

2) определим чистое время для движения 10-5-2=3 ч

потратил только на движение на лодке

пусть х расстояние от старта до того места, где бросил он якорь

, тогда время по течению равно х/(9+3) а против течения х/(9-3). Как мы выяснили время на движение лодки заняло 3 часа ⇒ получаем следующее уравнение:

х+2х=12×3

3х=36

х=12 км

ответ:12 км

1) Квадратичная функция y=x^2 ; график функции парабола, ветви направлены вверх, с центром в О (0;0), проходит через точки: (1;1) и (-1;1), (2; 4)  и (-2;4), (0; 1.5) и (-2; 1.5)

Линейная функция y=2x+3 ; график функции прямая, проходящая через точки (0;3) и  (2;7)

По заданным точкам строим 2 графика.

2) Для нахождения точек пересечения приравняем y=y и найдем точки на абциссе (х):

2x+3=x^2;

x^2-2x-3=0

а=1

b=-2

c=-3

D= 4+12 = 16, х>0, х1,х2,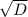 =4

х1= (-b+4)/2a= 3

х2= (-b-4)/2a= -1

Подставим найденные x в уравнение y=x^2 и найдем ординату (у), y1=9; y2=1. Так точки пересечения двух графиков: (3;9) и (-1; 1).

Запишем ответ x= -1; 3