1) a+b+c=0 => a+b=-c => (a+b)³=(-c)³ => a³+3a²b+3ab²+b³=-c³ => => a³+b³+c³=-(3a²b+3ab²) => a³+b³+c³=-3ab(a+b) => a³+b³+c³=-3ab(-c) => => a³+b³+c³=3abc 2) Обратное утверждение: Если a³+b³+c³=3abc, то a+b+c=0 (думаю, имеется в виду, что a+b+c обязательно будет равно 0, и не существует других вариантов). Из утверждения следует, что c³-3abc+a³+b³=0. Допустим, известны числа a и b. Тогда c³-3abc+a³+b³=0 является кубическим уравнением относительно c. Как известно, любое кубическое уравнение с рациональными коэффициентами имеет ровно три корня (необязательно действительных). Отсюда следует, что при фиксированных a и b и при 3-х вариантах c получится три варианта для суммы a+b+c, одним из которых является a+b+c=0. Таким образом, пункт 1 является верным. Пункт 2 не является верным. Найдем другие два варианта для c. Известно, что в уравнении c³-3abc+a³+b³=0 одним из решений является c=-(a+b), так как при подстановке в уравнение получится тождество. Разложим левую часть уравнения на скобки: c³-3abc+a³+b³=(a+b+c)(c²-c(a+b)+a²-ab+b²). Решим уравнение c²-c(a+b)+a²-ab+b²=0 относительно c: D=(-(a+b))²-4(a²-ab+b²)=a²+2ab+b²-4a²+4ab-4b²=-3(a²-2ab+b²)=-3(a-b)²≤0 c1,2=((a+b)+-√3(a-b)*i)/2, где i²=-1, i - мнимая единица. Если D=0, то a=b, а выражение для c примет такой вид: c=(a+b)/2=(a+a)/2=a. Получим, что в этом случае a=b=c, а сумма a+b+c=3a для любого a. Если D<0, то c1=(a+b)/2+i√3(a-b)/2, c2=(a+b)/2-i√3(a-b)/2. А возможные варианты для суммы станут такими: a+b+c=a+b+(a+b)/2+i√3(a-b)/2=3(a+b)/2+i√3(a-b)/2, или a+b+c=a+b+(a+b)/2-i√3(a-b)/2=3(a+b)/2-i√3(a-b)/2
ОДЗ:
4x^2+9x+5>=0
D=81-80=1
x1=-1
x2=-1.25
(=-00; -1.25] U [-1 +00)
2x^2+x-1>=0
D=1+8=9
(2x-1)(x+1)>=0
x=(-00 -1] U [1/2 +00)
x^2-1>=0
(х-1)(х+1)>=0
x=(-00 -1] U [1 +00)
Общее ОДЗ:
х={-1} U [1 +00)
4x^{2} +9x+5=3x^{2}-2+2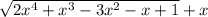
-2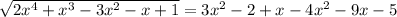
-2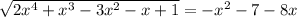
4(2x^{4}+x^{3}-3x^{2}-x+1)=x^{4}+49+64x^{2}+14x^{2}+16x^{3}+11x
8x^{4}+4x^{3}-12x^{2}-4x+4=x^{4}+49+78x^{2}+16x^{3}+112x
7x^{4}-12x^{3}-90x^{2}-116x-45=0
7x^{4}+7x^{3}-19x^{3}-19x^{2}-71x^{2}-71x-45x-45=0
7x^{3}*(x+1)-19x^{2}*(x+1)-71x*(x+1)-45(x+1)=0
(x+1)(7x^{3}-19x^{2}-71x-45)=0
(x+1)(7x^{3}+7x^{2}-26x^{2}-26x-45x-45)=0
(x+1)(7x^{2}*(x+1)-26x*(x+1)-45(x+1)=0
(x+1)^{2}*(7x^{2}-26x-45)=0
(x+1)^{2}*(7x^{2}+9x-35x-45)=0
(x+1)^{2}*(x(7x+9)-5(7x+9))=0
(x+1)^{2}*(7x+9)*(x-5)=0
(x+1)^{2}=0
x=-1
7x+9=0
x=- - не удовлетворяет ОДЗ
- не удовлетворяет ОДЗ
x-5=0
x=5
x=5
x=-1
=> a³+b³+c³=-(3a²b+3ab²) => a³+b³+c³=-3ab(a+b) => a³+b³+c³=-3ab(-c) =>
=> a³+b³+c³=3abc
2) Обратное утверждение:
Если a³+b³+c³=3abc, то a+b+c=0 (думаю, имеется в виду, что a+b+c обязательно будет равно 0, и не существует других вариантов).
Из утверждения следует, что c³-3abc+a³+b³=0. Допустим, известны числа a и b. Тогда c³-3abc+a³+b³=0 является кубическим уравнением относительно c. Как известно, любое кубическое уравнение с рациональными коэффициентами имеет ровно три корня (необязательно действительных). Отсюда следует, что при фиксированных a и b и при 3-х вариантах c получится три варианта для суммы a+b+c, одним из которых является a+b+c=0.
Таким образом, пункт 1 является верным. Пункт 2 не является верным.
Найдем другие два варианта для c.
Известно, что в уравнении c³-3abc+a³+b³=0 одним из решений является c=-(a+b), так как при подстановке в уравнение получится тождество. Разложим левую часть уравнения на скобки:
c³-3abc+a³+b³=(a+b+c)(c²-c(a+b)+a²-ab+b²).
Решим уравнение c²-c(a+b)+a²-ab+b²=0 относительно c:
D=(-(a+b))²-4(a²-ab+b²)=a²+2ab+b²-4a²+4ab-4b²=-3(a²-2ab+b²)=-3(a-b)²≤0
c1,2=((a+b)+-√3(a-b)*i)/2, где i²=-1, i - мнимая единица.
Если D=0, то a=b, а выражение для c примет такой вид: c=(a+b)/2=(a+a)/2=a. Получим, что в этом случае a=b=c, а сумма a+b+c=3a для любого a.
Если D<0, то c1=(a+b)/2+i√3(a-b)/2,
c2=(a+b)/2-i√3(a-b)/2.
А возможные варианты для суммы станут такими:
a+b+c=a+b+(a+b)/2+i√3(a-b)/2=3(a+b)/2+i√3(a-b)/2,
или
a+b+c=a+b+(a+b)/2-i√3(a-b)/2=3(a+b)/2-i√3(a-b)/2