У завданнях 1-6 виберіть правильну відповідь.
1. Якій із координатних осей належить точка A(0;-2;0) ?
А. Ox.
Б. Oy.
В. Oz.
Г. Жодній.
2. На якій відстані від початку координат розміщена точка A(-4;2;4)?
А. 2.
Б. 4.
В. 6.
Г. 36.
3. Яка з точок симетрична точці A(2;-3;4) відносно площини xy?
A. А 1 (2;-3;-4).
Б. A 1 (-2;3;-4).
B. A 1 (-2;3;4).
Г. A 1 (2;3;4).
4. Від точки A відкладено вектор АВ =а. Знайдіть координати точки B, якщо А(-1;5;0),
а(1;-3;0)
A. B(2;2;0)
Б. B(0;8;0).
B. B(0;2;0).
Г. B(-2;-2;0).
5. Задано точки M(-1;4;3), N(-2;5;-2), K(3;-4;6), P(2;-3;1). Яке з наведених тверджень
правильне?
А.АВ=РК
Б. MN= -2PK
B. MN=1/2PK
Г. MN=KP
6. При якому значенні n вектори a (3;-5;n) і b (n;1;2) перпендикулярні?
А. 1.
Б. -1.
В. -5.
Г. 3.
Достатній рівень ( )
7. У прямокутній системі координат у задано точки A(2;4;-2) і B(4;-2;6).
Установіть відповідність між початком речення (1-4) і його закінченням (А-Д) так, щоб
утворилось правильне твердження:
1 Проекцією точки A на вісь Ox є точка А (3;1;2)
2 Проекцією точки B на площину xz є точка Б (4;0;6)
3 Серединою відрізка AB є точка В (0;-2;6)
4 ВекторАВ має координати Г (2;0;0)
Д (2;-6;8)
8. Знайдіть довжину вектора а=р - 4k, якщо р (6;-5;3), k (2;-1;1)
Високий рівень ( )
Наведіть повне розв'язання задачі 9.
9. Задано точки A(1;4;8) і B(-4;0;3). Знайдіть косинус кута, під яким відрізок AB видно з
початку координат.
1. Решим первое неравенство этой системы:
ответ: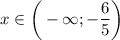
2. Дробь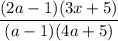 существует, если
существует, если
Перед тем как выражать , нужно рассмотреть случаи, когда дробь
, нужно рассмотреть случаи, когда дробь 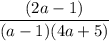 положительная, а когда отрицательная:
положительная, а когда отрицательная:
Если такая дробь положительная, то при нахождении переменнойРешим неравенство методом интервалов.
а) ОДЗ: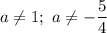
б) Нуль неравенства: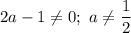
в) Решением данного неравенства будет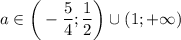 .
.
При таких значениях параметра знак неравенства меняться не будет:
знак неравенства меняться не будет:
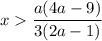
Если такая дробь отрицательная, то при нахождении переменнойРешим неравенство методом интервалов. Решением данного неравенства будет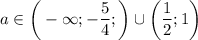 .
.
При таких значениях параметра знак неравенства изменится:
знак неравенства изменится:
ответ: если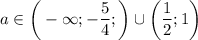 , то
, то 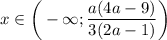 ; если
; если 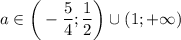 , то
, то 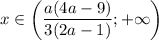 ; если
; если 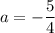 и
и 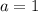 , то неравенство не имеет решений.
, то неравенство не имеет решений.
3. Данная система неравенств решается в зависимости от значений параметра , поэтому:
, поэтому:
1) Рассмотрим случай, когда решение неравенств пересекается:
Если2) Рассмотрим случай, когда решение неравенств не пересекается (когда система не имеет решений):
Оставшийся промежуток является решением этого варианта:ответ: если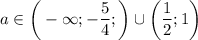 , то
, то 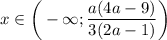 ; если
; если 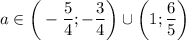 , то
, то 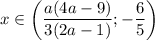 ; если
; если ![a \in \bigg[-\dfrac{3}{4}; \dfrac{1}{2} \bigg]\cup \bigg[\dfrac{6}{5}; + \infty \bigg) \cup \begin{Bmatrix} -\dfrac{5}{4}; 1 \end{Bmatrix}](/tpl/images/0595/8885/89750.png) , то система не имеет решений.
, то система не имеет решений.
2/3; 2
Объяснение:
3y^2-8y+4=0
D=(-8)^2-4*3*4=64-48=16
В уравнении 2 корня, значит
x1 = (-(-8) +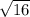 )/(2*3) = 12/6 = 2 - первый корень
)/(2*3) = 12/6 = 2 - первый корень
x2 = (-(-8) -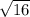 )/(2*3) = 4/6 = 2/3 - второй корень
)/(2*3) = 4/6 = 2/3 - второй корень
Как найти дискриминант?
1) Дискриминант квадратного уравнения ax^2+bx+c находится по формуле: b^2-4ac. a; b и c - коэффициенты. В данном случае a=3; b=-8; c=4.
2) Подставляем: D=(-8)^2-4*(3*4)=64-48=16
3) Если D>0, то в уравнении 2 корня, если D=0, то в уравнении 1 корень, если D<0, то в уравнении корней нет
Как найти корни?
Опять же таки берём уравнение вида ax^2+bx+c
Если D>0, то x1 = (-b+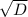 )/2a
)/2a
x2 = (-b-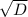 )/2a
)/2a
Если D=0, то x = -b/2a
Если D<0, то ничего не ищем
P.S. Также есть теоремы Виета и выделения полного квадрата, но они более замороченные. Конечно, проще решать через дискриминант, но если вы хотите увидеть, как решить уравнение другим напишите, я отредактирую ответ, попробую решить другим