У ящика лежать 48 деталей, із них-17 деталей третього ґатунку ,19-другого ґатунку,а решта-першого.скількома можна обрати деталей першого або другого ґатунку? А.12 Б.228 В.36 Г.3й
Для того чтобы геометрическая прогрессия была бесконечно убывающей, знаменатель геометрической прогрессии должен быть либо меньше 0, но больше -1, либо больше 0, но меньше 1. В таком случае геометрическая прогрессия будет стремиться к 0, но никогда его не достигнет.
Графически это выглядит так: или .
Рассмотрим наши примеры:
1) . Выполняются ли условия неравенства?
. Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.
2) . Выполняются ли условия неравенства?
. Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.
3) . Выполняются ли условия неравенства?
. Да, выполняются. Данная геометрическая прогрессия является бесконечно убывающей.
Для того чтобы геометрическая прогрессия была бесконечно убывающей, знаменатель геометрической прогрессии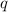 должен быть либо меньше 0, но больше -1, либо больше 0, но меньше 1. В таком случае геометрическая прогрессия будет стремиться к 0, но никогда его не достигнет.
должен быть либо меньше 0, но больше -1, либо больше 0, но меньше 1. В таком случае геометрическая прогрессия будет стремиться к 0, но никогда его не достигнет.
Графически это выглядит так: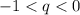 или
или 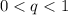 .
.
Рассмотрим наши примеры:
1)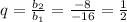 . Выполняются ли условия неравенства?
. Выполняются ли условия неравенства?
2)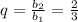 . Выполняются ли условия неравенства?
. Выполняются ли условия неравенства?
3)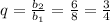 . Выполняются ли условия неравенства?
. Выполняются ли условия неравенства?
Объяснение:
а) домножить числитель и знаменатель на (√2+1)
получится (√2+1) /(2-1) (в знаменателе разность квадратов) Для этого всегда домножаем на сопряженное) ответ (√2+1)
б) домножь (√3+1) получишь 2(√3+1)/3-1 = (√3+1)
в) домножь (√5-1) получишь (√5-1)²/5-1 = (√5-1)²/4=5-2√5+1/4=2(3-√5)/4=
(3-√5)/2
г) домножь на √3+1 и получишь (√3+1)²/2=3+2√3+1/2=2+√3
д) домножь на √3-√2 получишь √3-√2 /1=√3-√2
е) домножь на √5-√3 и получишь (√5-√3)² / 2 = 5-2√15+3/2=4-√15
2) 5√2/10=√2/2 б) делим на √2 получим √2+1
в) делим на √5 (5=√5·√5) получим 1+√5