Это тождество Эйлера, являющееся частным случаем формулы Эйлера при .
Тождество объединяет между собой пять фундаментальных чисел из разных областей математики, связь между которыми на первый взгляд неочевидна:
1) основание натурального логарифма (алгебра);
2) отношение длины окружности к ее диаметру (геометрия);
3) мнимую единицу (комплексные числа);
4) нейтральный элемент относительно умножения 1 (арифметика);
5) нейтральный элемент относительно сложения 0 (арифметика).
Тождество примечательно в первую очередь своей простотой и элегантностью. Так, Ричард Фейнманн называл его "самой замечательной формулой в математике".
Примечательна фраза профессора Гарвардского университета Бенджамин Пирса, произнесенная после доказательства тождества Эйлера: "мы не можем понять её [формулу], и мы не знаем, что она значит, но мы доказали её, и поэтому мы знаем, что она должна быть достоверной".
Объяснение:
Найдем уравнение параболы, для этого подставим координаты точек (1;4) (2;5) (3;2) в уравнение g(x)=ax²2+bx+c, получим систему уравнений
a+b+c=4
4a+2b+c=5
9a+3b+c=2
Решим методом сложения - вычитания
Первое уравнение умножим на -4 и -9 и сложим соответcтвенно со вторым и третьим уравнением
-4a-4b-4c=-16
+
4a+2b+c=5
-2b-3c=-11 (1)
-9a-9b-9c=-36
+
9a+3b+c=2
-6b-8c=-34 (2)
Уравнения (1) и (2) запишем как систему
-2b-3c=-11 (1)
-6b-8c=-34 (2)
Первое уравнение умножим на -3 и сложим со вторым
-2b-3c=-11
2b=11-3c
6b+9c=33
+
-6b-8c=-34
с=-1
Подставим с=-1 в уравнение -2b-3c=-11
-2b+3=-11
-2b=-14
b=-14/-2 =7
b=7
подставим с=-1 и b=7 в уравнение a+b+c=4
a+7-1=4
a+6=4
a=4-6
a=-2
Получили коэффициенты квадратного уравнения
a=-2 ; с=-1 ; b=7
Подставим коэффициенты в g(x)=ax²2+bx+c, получим
g(x)=-2x²+7x-1
Найдем точки пересечения
функций f(x)=−7x+19 и g(x)=-2x²+7x-1
Приравняем правые части
−7x+19=-2x²+7x-1
2x²-14x+20=0 поделим на 2
x²-7x+10=0
по теореме Виета x₁=2 ; x₂=5
x₁=2 это абсцисса точки А
x₂=5 это абсцисса точки В
подставим x₂=5 в уравнение f(x)=−7x+19
f(5)=-7*5+19=-35+19=-16 Это ордината точки В
ответ -16
Это тождество Эйлера, являющееся частным случаем формулы Эйлера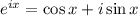
при 
.
Тождество объединяет между собой пять фундаментальных чисел из разных областей математики, связь между которыми на первый взгляд неочевидна:
1) основание натурального логарифма
(алгебра);
2) отношение длины окружности к ее диаметру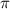
(геометрия);
3) мнимую единицу
(комплексные числа);
4) нейтральный элемент относительно умножения 1 (арифметика);
5) нейтральный элемент относительно сложения 0 (арифметика).
Тождество примечательно в первую очередь своей простотой и элегантностью. Так, Ричард Фейнманн называл его "самой замечательной формулой в математике".
Примечательна фраза профессора Гарвардского университета Бенджамин Пирса, произнесенная после доказательства тождества Эйлера: "мы не можем понять её [формулу], и мы не знаем, что она значит, но мы доказали её, и поэтому мы знаем, что она должна быть достоверной".