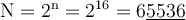У натурального числа N посчитали произведение всех его натуральных делителей (включая его самого). Оказалось, что максимальная степень двойки, на которую делится полученное число – 2^134. Найдите наименьшее N с таким свойством. В ответе укажите четыре последние цифры числа N.
ответ: N=65536 последние четыре цифры 5536
Объяснение:
Раз число N должно быть наименьшим то при разложении его на множители должны быть только двойки
Тогда произведение всех делителей числа можно представить в таком виде :
А число N=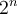
Тогда выйдет что :
Выходит арифметическая прогрессия :
где n -наименьшее натуральное число при котором выполняется неравенство
пусть :
Из чего исходя