У конкурсі «Ерудит» брали участь учні восьмого і дев'ятого класів. Кожен клас для оформлення роботи отримав 60 акушів паперу. Кожен учень восьмого класу отримав на 1 аркуш паперу менше, ніж кожен учень дев'ятого класу.

Решите неравенство:
А) (х-1)(х-3)≥0
x=1  x=3
x∈(-∞;1] U [3;∞)
Б)х(2-х)<0
x=0 x=2
x∈(-∞;0) U (2;∞)
Решите неравенство:
А) х²-4х+3≥0
x1+x2=4 U x1*x2=3⇒x1=1 U x2=3
x∈(-∞;1} U {3;∞)
Б)х(х²-9)<0
x(x-3)(x+3)<0
x=0  x=3 x=-3
         _                  +                _                  +
(-3)(0)(3)
x∈(-∞;-3) U (1;3)
Решите неравенство: (3х+1)/(2-х) <2
(3x+1)/(2-x)-2<0
(3x+1-4+2x)/(2-x)<0
(5x-3)/(2-x)<0
x=0,6  x=2
x∈(-∞;0,6) U (2;∞)
Найдите область определения функции:
А)у=√(3-х)
3-x≥0⇒x≤3
D(y)∈(-∞;3]
Б)у = 2/(х² -9)
x²-9≠0
x²≠9
x≠3
x≠-3
D(y)∈(-∞;-3) U (-3;3) U (3;∞)

 или

Объяснение:

Модуль раскрывается двумя вариантами: со знаком + или со знаком - . В этой задаче 2 модуля, следовательно максимум может быть 4 раскрытия.  

На практике имеем 3 области:

Область не существует, т.к. нет пересечений у неравенств, задающих область.

Рассмотрим каждый из трех случаев:

Получили решение, лежащее в области: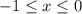

Получили неравенство, выполненное для любого x из этой области. Следовательно решение в этой области - сама область: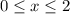

Получили решение, лежащее в области: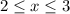

"Сшиваем" полученные решение и получаем:

 или