Пусть x рублей стоит пирожок, а y рублей - булка. Зная, что на 40 рублей можно купить три пирожка и две булки, составим первое уравнение системы: 3x+2y=40. Также, по условию задачи известно, что на 45 рублей можно приобрести два пирожка и три булки; составим второе уравнение системы: 2x+3y=45. Составим и решим систему уравнений:
6x+4y-6x69y=80-135 5y=55 y=11
ответ: 11 рублей стоит булка; 6 рублей стоит пирожок.
Пусть x - число девочек в классе, а y - мальчков. Зная, что всего в классе 24 ученика, составим первое уравнение: x+y=24. По условию задачи, чтобы девочкам выдать по три тетради,а мальчикам по две тетради,потребуется 59 тетрадей. Составим второе уравнение: 3x+2y=59. Составим систему уравнений:
Пусть x рублей стоит пирожок, а y рублей - булка. Зная, что на 40 рублей можно купить три пирожка и две булки, составим первое уравнение системы: 3x+2y=40. Также, по условию задачи известно, что на 45 рублей можно приобрести два пирожка и три булки; составим второе уравнение системы: 2x+3y=45. Составим и решим систему уравнений:
6x+4y-6x69y=80-135
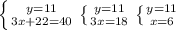
5y=55
y=11
ответ: 11 рублей стоит булка; 6 рублей стоит пирожок.
Пусть x - число девочек в классе, а y - мальчков. Зная, что всего в классе 24 ученика, составим первое уравнение: x+y=24. По условию задачи, чтобы девочкам выдать по три тетради,а мальчикам по две тетради,потребуется 59 тетрадей. Составим второе уравнение: 3x+2y=59. Составим систему уравнений:
3x+2y-2x-2y=59-48
x=11
ответ: в классе 11 девочек, 13 мальчиков.
1.
6sin^2x-3sinx*cosx-cos^2x=sin^2x+cos^2x
5sin^2x-3sinx*cosx-2cos^2x=0 /:cos^2x≠0
5tg^2x-3tgx-2=0
замена tgx=t
5t^2-3t-2=0
t=1
t=-2/5
обратная замена:
1) tgx=1
x=pi/4+pik, k∈Z
2) tgx=-2/5
x=-arctg(2/5)+pik, k∈Z
pi/4+pik, k∈Z
-arctg(2/5)+pik, k∈Z
2.
5sin^2x+3sinx*cosx-2cos^2x=3sin^2x+3cos^2x
2sin^2x+3sinx*cosx-5cos^2x=0 /:cos^2x≠0
2tg^2x+3tgx-5=0
замена tgx=t
2t^2+3t-5=0
t=1
t=-5/2
обратная замена:
1) tgx=1
x=pi/4+pik, k∈Z
2) tgx=-5/2
x=-arctg(5/2)+pik, k∈Z
pi/4+pik, k∈Z
-arctg(5/2)+pik, k∈Z