Войти
Регистрация
Спроси ai-bota
В
Все
Б
Биология
Б
Беларуская мова
У
Українська мова
А
Алгебра
Р
Русский язык
О
ОБЖ
И
История
Ф
Физика
Қ
Қазақ тiлi
О
Окружающий мир
Э
Экономика
Н
Немецкий язык
Х
Химия
П
Право
П
Психология
Д
Другие предметы
Л
Литература
Г
География
Ф
Французский язык
М
Математика
М
Музыка
А
Английский язык
М
МХК
У
Українська література
И
Информатика
О
Обществознание
Г
Геометрия
Показать больше
Показать меньше
Ilyavazhnov1995
17.04.2020 04:03 •
Алгебра
найти корни из компл.чисел
Показать ответ
Ответ:
oksankavdovina
09.10.2020 12:44
Рассмотрим комплексное число
, его модуль
. Тогда
Поскольку
то
0,0
(0 оценок)
Популярные вопросы: Алгебра
paraxatdin
29.09.2022 05:48
1) может ли график уравнения с двумя переменными состоять только из одной точки? 2) какая фигура является графиком уравнения y=kx+b?...
butterfly31
29.09.2022 05:48
Решите : купили несколько книг и пытаются разместить их на одинаковых полках в книжном шкафу. сначала поставили по 20 книг на каждую полку. в результате две полки остались...
HesteVlad
29.09.2022 05:48
Впараллелограмме klmn диагональ ln образует 58° со стороной kl и 63°со сторрной lm.найти угл m...
EVETS1
09.10.2021 14:07
Не возводя число степень сравните значения выражений (4 дропь 3)степень4 и (4 дропь3)степень4...
Nazerke0606
26.08.2020 13:31
Вариант 2 1. Разложите на множители: 1) 27x3 − y3; 3) −3x2 − 12x − 12; 2) 25a3 − ab2; 4) 3ab − 15a + 12b − 60; 5) a4 − 625. 2. Упростите выражение x(x − 1)(x + 1) − (x...
Assel0802
14.11.2020 23:18
Найти значение выражения ! ...
tatianadettcel
31.03.2021 08:54
28sin20 cos20/sin40 найдите значение выражения! , !...
Manya081505
03.10.2022 14:10
4. прямолинейное движение точки описывается законом s=t5 – t3(м). найдите ее скорость в момент времени t=2с....
кристина2059
19.07.2022 03:24
{3m+2n=7 {m-2n=-3 {7а-3в/5=-4{а+2в/5=-4решите подстановки...
polykoly
24.02.2023 08:32
Задайте формулой функцию, график которой проходит через точку (0; 4) и параллелен графику функции y = –3x. c объяснением...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Рассмотрим комплексное число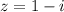 , его модуль
, его модуль 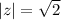 . Тогда
. Тогда
Поскольку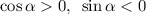 то
то