1. Упростить выражения нельзя, поэтому просто подставим
4
Теперь с другим знаком, на деле это будет вторая дробь, только у а противположный знак
во втором примере удобно представить икс и игрик в виде направильных дробей, тогда 1= -2=-
произведем вычисления 11*3/6=11/2
-11*2/4=11/2.
11/2-11/2=0
2. Выражение представленное в виде дроби имеет смысл тогда и только тогда, когда знаменатель не равен нулю, соответственно
А-3, т.к. если икс равен минус 2, то 2-2=0 а на 0 делить нельзя
Б-4, т.к. в знаменателе перменной нет
В -2, т.к. произведение двух выражений равно нулю, когда хотя бы 1 равен нулю, а значит чтобы произведение не было равно нулю, то ни одно из них не должно равнятся нулю, отсюда исключаем 2 и -2
11sin^2 a + 9cos^2 a + 8sin^4 a + 2cos^4 a = = 9sin^2 a + 9cos^2 a + 2sin^2 a + 6sin^4 a + 2(sin^4 a + 2cos^4 a) = (*) Заметим, что 1) 9sin^2 a + 9cos^2 a = 9(sin^2 a + cos^2 a) = 9 2) sin^4 a + cos^4 a = sin^4 a + 2sin^2 a*cos^2 a + cos^4 a - 2sin^2 a*cos^2 a = = (sin^2 a + cos^2 a)^2 - 2sin^2 a*cos^2 a = 1 - 1/2*(4sin^2 a*cos^2 a) Подставляем (*) = 9 + 2sin^2 a + 6sin^4 a + 2 - 4sin^2 a*cos^2 a = = 11 + 4sin^2 a - 2sin^2 a + 6sin^4 a - 4sin^2 a*cos^2 a = = 11 - 2sin^2 a + 6sin^4 a + 4sin^2 a*(1 - cos^2 a) = = 11 - 2sin^2 a + 6sin^4 a + 4sin^4 a = 11 - 2sin^2 a + 10sin^4 a = = 10(sin^4 a - 2*1/10*sin^2 a + 1/100) - 1/10 + 11 = = 10(sin^2 a - 1/10)^2 + 109/10 Минимальное значение квадрата равно 0, а всего выражения 109/10.
Объяснение:
1. Упростить выражения нельзя, поэтому просто подставим
Теперь с другим знаком, на деле это будет вторая дробь, только у а противположный знак
во втором примере удобно представить икс и игрик в виде направильных дробей, тогда 1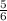 =
=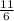 -2
-2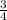 =-
=-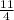
произведем вычисления 11*3/6=11/2
-11*2/4=11/2.
11/2-11/2=0
2. Выражение представленное в виде дроби имеет смысл тогда и только тогда, когда знаменатель не равен нулю, соответственно
А-3, т.к. если икс равен минус 2, то 2-2=0 а на 0 делить нельзя
Б-4, т.к. в знаменателе перменной нет
В -2, т.к. произведение двух выражений равно нулю, когда хотя бы 1 равен нулю, а значит чтобы произведение не было равно нулю, то ни одно из них не должно равнятся нулю, отсюда исключаем 2 и -2
= 9sin^2 a + 9cos^2 a + 2sin^2 a + 6sin^4 a + 2(sin^4 a + 2cos^4 a) = (*)
Заметим, что
1) 9sin^2 a + 9cos^2 a = 9(sin^2 a + cos^2 a) = 9
2) sin^4 a + cos^4 a = sin^4 a + 2sin^2 a*cos^2 a + cos^4 a - 2sin^2 a*cos^2 a =
= (sin^2 a + cos^2 a)^2 - 2sin^2 a*cos^2 a = 1 - 1/2*(4sin^2 a*cos^2 a)
Подставляем
(*) = 9 + 2sin^2 a + 6sin^4 a + 2 - 4sin^2 a*cos^2 a =
= 11 + 4sin^2 a - 2sin^2 a + 6sin^4 a - 4sin^2 a*cos^2 a =
= 11 - 2sin^2 a + 6sin^4 a + 4sin^2 a*(1 - cos^2 a) =
= 11 - 2sin^2 a + 6sin^4 a + 4sin^4 a = 11 - 2sin^2 a + 10sin^4 a =
= 10(sin^4 a - 2*1/10*sin^2 a + 1/100) - 1/10 + 11 =
= 10(sin^2 a - 1/10)^2 + 109/10
Минимальное значение квадрата равно 0, а всего выражения 109/10.